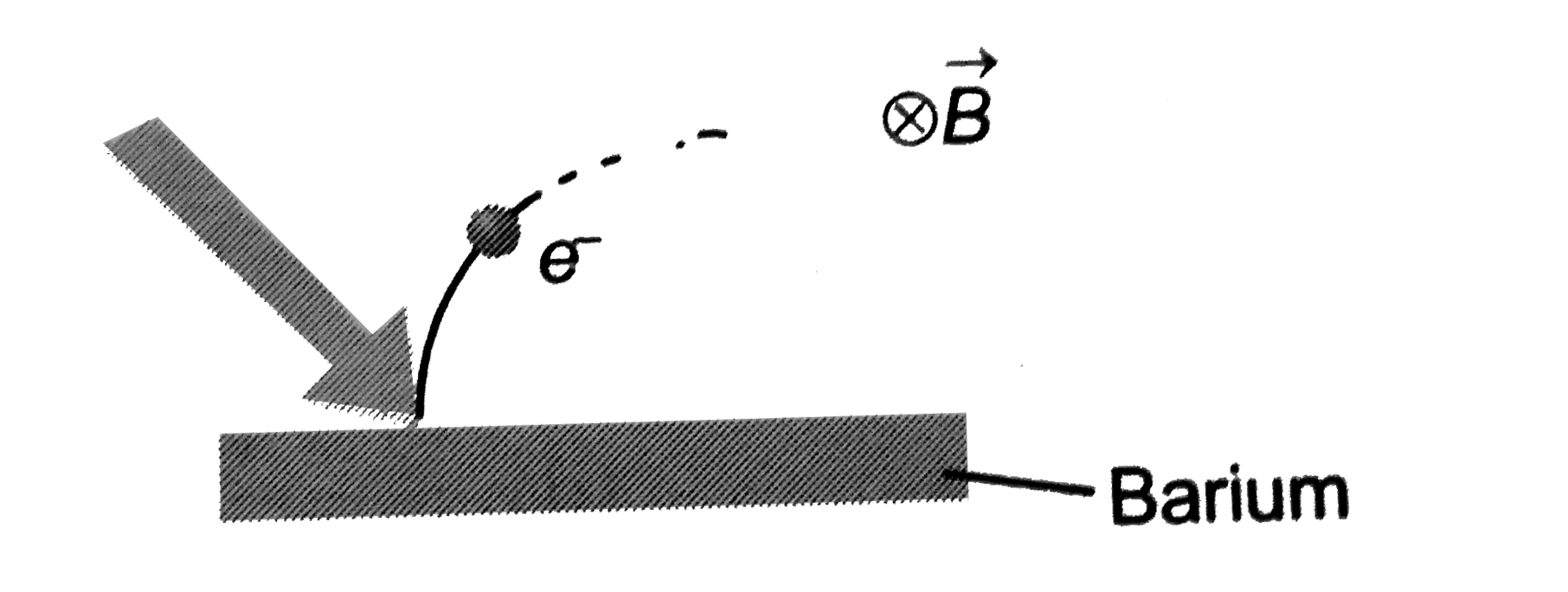
When barium is irradiated by a light of λ=4000A all the photoelectrons emitted are bent in a circle of radius 50 cm by a magnetic field of flux density 5.26×10−6 T acting perpendicular to plane of emission of photoelectron. Then,
the kinetic energy of fastest photoelectrin is 0.6 eV
work function of the metal is 2.5 eV
the maximum velocity of photoelectron is 0.46×106ms−1
the stopping potential for photoelectric effect is 0.6 V
The correct Answer is:A, B, C, D
To solve the problem step by step, we will follow the logical sequence of calculations based on the information provided.
Step 1: Calculate the Velocity of Photoelectrons
The formula for the velocity V of the photoelectrons in a magnetic field is given by:
V=B⋅q⋅Rm
Where:
- B=5.26×10−6T (magnetic flux density)
- q=1.6×10−19C (charge of an electron)
- R=0.5m (radius of the circular path)
- m=9.1×10−31kg (mass of an electron)
Substituting the values into the formula:
V=(5.26×10−6)⋅(1.6×10−19)⋅(0.5)9.1×10−31
Calculating this gives:
V≈0.46×106m/s
Step 2: Calculate the Kinetic Energy of the Photoelectrons
The kinetic energy K of the photoelectrons is given by:
K=12mV2
Substituting the values:
K=12⋅(9.1×10−31)⋅(0.46×106)2
Calculating this gives:
K≈0.962×10−19J
Step 3: Convert Kinetic Energy to Electron Volts
To convert the kinetic energy from joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
Ke=0.962×10−191.6×10−19≈0.6eV
Step 4: Calculate the Stopping Potential
The stopping potential Vs is equal to the kinetic energy in electron volts:
Vs=0.6V
Step 5: Calculate the Work Function
The work function W can be calculated using the formula:
Ke=hcλ−W
Where:
- h=4.14×10−15eV s
- c=3×108m/s
- λ=4000Å=4000×10−10m
Calculating hcλ:
hcλ=(4.14×10−15)⋅(3×108)4000×10−10≈2.5eV
Now substituting back to find W:
0.6=2.5−W⟹W=2.5−0.6=1.9eV
Summary of Results
- Velocity of photoelectrons: 0.46×106m/s
- Kinetic Energy: 0.6eV
- Stopping Potential: 0.6V
- Work Function: 1.9eV
The formula for the velocity V of the photoelectrons in a magnetic field is given by:
- B=5.26×10−6T (magnetic flux density)
- q=1.6×10−19C (charge of an electron)
- R=0.5m (radius of the circular path)
- m=9.1×10−31kg (mass of an electron)
The kinetic energy K of the photoelectrons is given by:
To convert the kinetic energy from joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
The stopping potential Vs is equal to the kinetic energy in electron volts:
The work function W can be calculated using the formula:
- h=4.14×10−15eV s
- c=3×108m/s
- λ=4000Å=4000×10−10m
- Velocity of photoelectrons: 0.46×106m/s
- Kinetic Energy: 0.6eV
- Stopping Potential: 0.6V
- Work Function: 1.9eV
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer
9 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Single Correct
130 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
When 0.50 Å X-ray strike a material , the photoelectron from the K shell are observed to move in a circle of radius 2.3nm in a magnetic field of 2×10−2 tesle acting perpendicular to direct of emission of photoelectron . What is the binding elergy of k−shell electron?
View SolutionWhen 24.8keV X- rays strike a material, the photoelectrons emitted from K shell are observed to move in a circle of radius 23 mm in a magnetic field of 2×10−2T. The binding energy of K shell electrons is
View SolutionLight of wavelength 4000Å is incident on barium. Photoelectrons emitted describe a circle of radius 50 cm by a magnetic field of flux density 5.26×10−6tesla. What is the work function of barium in eV? Given h=6.6×10−34Js,e=1.6×10−19C,me=9.1×10−31kg.
View SolutionLight of wavelength 2475Å is incident on barium. Photoelectrons emitted describe a circle of radius 100cm by a magnetic field of flux density 1√17×10−5Tesla.
Work function of the barium is (Given em=1.7×1011)
View SolutionA current - carrying circular coil of 100 turns and radius 5.0 cm produces a magnetic field of (6.0×10−5) T at its centre. Find the value of the current.
View SolutionCalculate torque acting on a bar magnet of length 20 cm magnetic dipole moment 4×10−6Am2 , which is placed in earth's magnetic field of flux density 2×10−5T , perpendicular to the field .
View SolutionA semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
View SolutionA rectangular coil having 60 turns and area of 0.4 m2 is held at right angles to a uniform magnetic field of flux density 5×10−5T. Calculate the magnetic flux passing through it.
View SolutionWhen an atom X absorbs radiation with a photon energy than the ionization energy of the atom, the atom is ionized to generate an ion X+ and the electron (called a photoelectron) is ejected at the same time. In this event, the energy is conserved as shown in Figure 1, that is,
Photon energy (h)=ionization energy (IE) of X+ kinetic energy of photoelectron.
When a molecule, for example, H2, absorbs short-wavelength light, the photoelectron is ejected and an H2, ion with a variety of vibrational states is produced. A photoelectron spectrum is a plot of the number of photoelectrons as a function of the kinetic energy of the photoelectrons. Figure-2 shows a typical photoelectron spectrum when H2 in the lowest vibrational level is irradiated by monochromatic light of 21.2eV. No photoelectrons are detected above 6.0eV. (eV is a unit of energy and 1.0eV is equal to 1.6×10−19J)
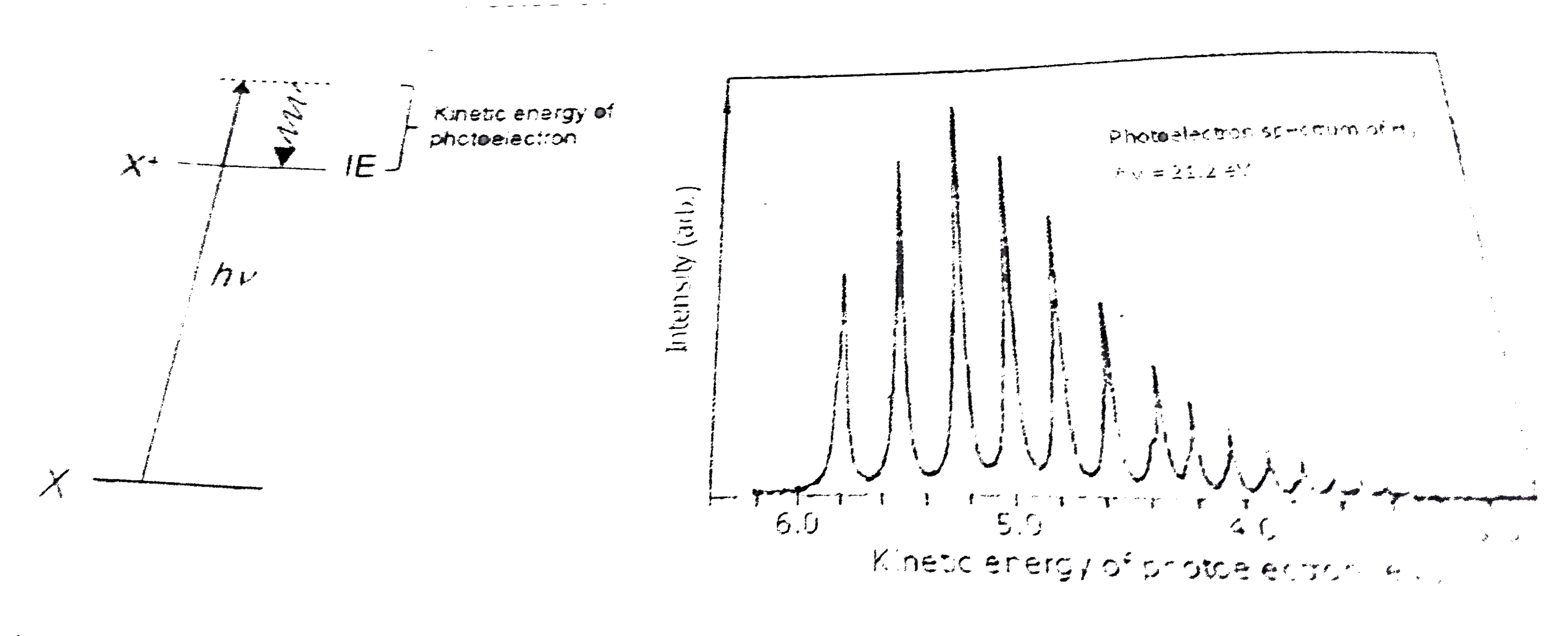
Figure 1 Schematic diagram of photoelectron spectroscopy.
Figure 2 Photoelectron spectrum of H2. The energy of the incident light is 21.2eV
Considering an energy cycle, determine––––––––––– the bond energy ED(eV) of H+2 to the first decimal place. If you were unable to determine the values for EB and EC, then use 15.0eV and 5.0eV for EB and EC, respectively.
View SolutionWhen an atom X absorbs radiation with a photon energy than the ionization energy of the atom, the atom is ionized to generate an ion X+ and the electron (called a photoelectron) is ejected at the same time. In this event, the energy is conserved as shown in Figure 1, that is,
Photon energy (h)=ionization energy (IE) of X+ kinetic energy of photoelectron.
When a molecule, for example, H2, absorbs short-wavelength light, the photoelectron is ejected and an H2, ion with a variety of vibrational states is produced. A photoelectron spectrum is a plot of the number of photoelectrons as a function of the kinetic energy of the photoelectrons. Figure-2 shows a typical photoelectron spectrum when H2 in the lowest vibrational level is irradiated by monochromatic light of 21.2eV. No photoelectrons are detected above 6.0eV. (eV is a unit of energy and 1.0eV is equal to 1.6×10−19J)
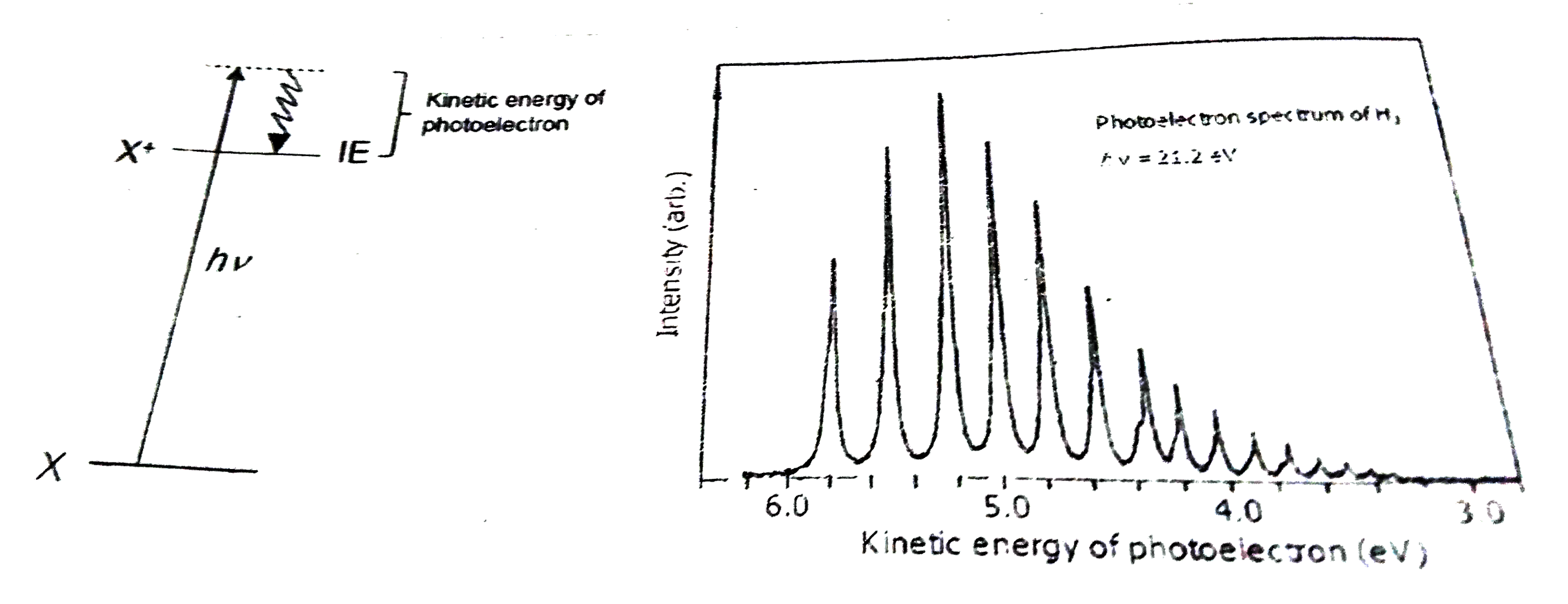
Figure 1 Schematic diagram of photoelectron spectroscopy.
Figure 2 Photoelectron spectrum of H2. The energy of the incident light is 21.2eV
Determine–––––––––––– the bond energy EC(eV) of H2 to the first decimal place.
View Solution
