A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
To find the magnitude of the magnetic force acting on a semicircular wire carrying a current in a magnetic field, we can follow these steps:
1. Identify the Given Values:
- Radius of the semicircular wire, R=5.0cm=0.05m
- Current flowing through the wire, I=5.0A
- Magnetic field strength, B=0.50T
2. Calculate the Length of the Semicircular Wire:
- The length of the semicircular wire can be calculated using the formula for the circumference of a circle. The length L of the semicircular wire is given by:
L=12×2πR=πR
- Plugging in the radius:
L=π×0.05m≈0.157m
3. Determine the Force on the Wire:
- The magnetic force F on a current-carrying wire in a magnetic field is given by the formula:
F=ILBsin(θ)
- Here, θ is the angle between the direction of the current and the magnetic field. Since the magnetic field is perpendicular to the plane of the wire, θ=90∘ and sin(90∘)=1.
- Therefore, the force can be simplified to:
F=ILB
4. Substituting the Values:
- Now substituting the known values into the equation:
F=5.0A×0.157m×0.50T
- Calculating this gives:
F=5.0×0.157×0.50=0.3925N
5. Final Result:
- The magnitude of the magnetic force acting on the semicircular wire is approximately:
F≈0.39N
Summary:
The magnitude of the magnetic force acting on the semicircular wire is approximately 0.39 N.
- Radius of the semicircular wire, R=5.0cm=0.05m
- Current flowing through the wire, I=5.0A
- Magnetic field strength, B=0.50T
- The length of the semicircular wire can be calculated using the formula for the circumference of a circle. The length L of the semicircular wire is given by:
L=12×2πR=πR
- Plugging in the radius:
L=π×0.05m≈0.157m
- The magnetic force F on a current-carrying wire in a magnetic field is given by the formula:
F=ILBsin(θ)
- Here, θ is the angle between the direction of the current and the magnetic field. Since the magnetic field is perpendicular to the plane of the wire, θ=90∘ and sin(90∘)=1.
- Therefore, the force can be simplified to:
F=ILB
- Now substituting the known values into the equation:
F=5.0A×0.157m×0.50T
- Calculating this gives:
F=5.0×0.157×0.50=0.3925N
- The magnitude of the magnetic force acting on the semicircular wire is approximately:
F≈0.39N
The magnitude of the magnetic force acting on the semicircular wire is approximately 0.39 N.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
A wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View Solution
Knowledge Check
- Question 1 - Select One
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44N
A wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of radius 4.0 cm as shown in . A wire, carrying a current of 2.0 A, is placed perpendiuclar to and intersecting the axis of the cylindreical region. Find the magnitude of the force acting on the wire.
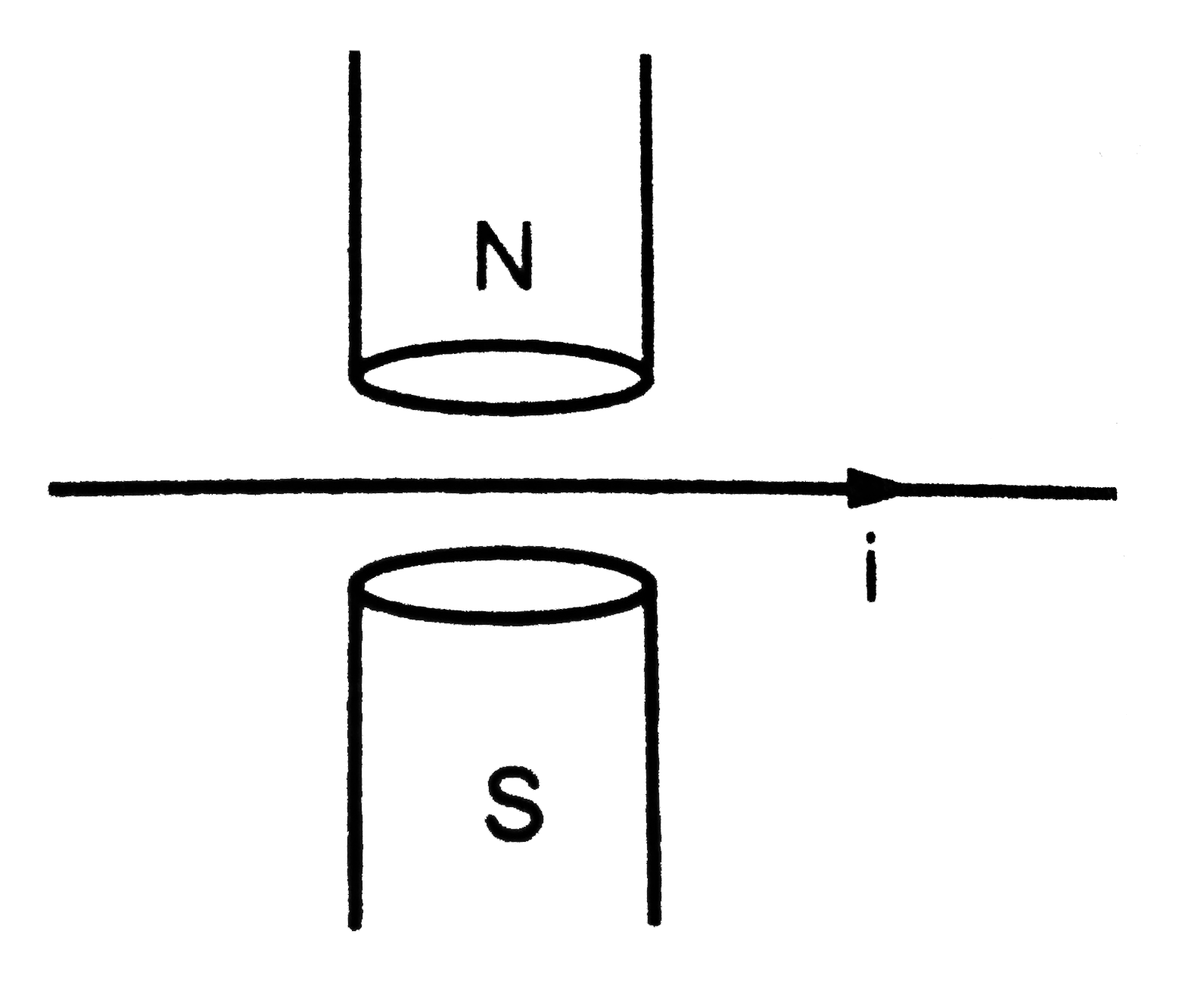 View Solution
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
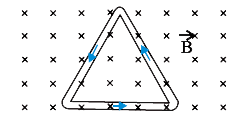 View Solution
View SolutionA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
View SolutionA current loop, carrying a current of 5.0 A, is in the shape of a right triangle with sides 30,40, and 50 cm. The loop is in a uniform magnetic field of magnitude 80 mT whose direction is parallel to the current in the 50 cm side of the loop. Find the magnitude of (a) the magnetic dipole moment of the loop and (b) the torque on the loop.
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m
 View Solution
View Solution

