When the angle of inclination of on inclined plane is θ, an object slides down with uniform velocity. If the same object is pushed up with an initial velocity u on the same inclined plane, it goes up the plane and stops at a certain distance on the plane. There after the body.
Slides down the inclined plane and reaches the ground. With velocity "u"
Slides down the inclined plane and reaches the ground with velocity less than "u"
Slides down the inclined plane and reaches the ground with velocity greater than "u"
Stays at rest on the inclined plane and will not side down.
The correct Answer is:D
To solve the problem, we need to analyze the motion of the object on the inclined plane under the influence of forces acting on it. Here's a step-by-step solution:
Step 1: Understand the Forces Acting on the Object
When the object slides down the inclined plane with uniform velocity, it means that the net force acting on the object is zero. The forces acting on the object are:
- The gravitational force component acting down the incline: Fgravity=mgsinθ
- The frictional force acting up the incline: Ffriction=f
Since the object is moving with uniform velocity, we have:
Fgravity=Ffriction
Thus,
mgsinθ=f
Step 2: Analyze the Situation When Pushed Up the Incline
Now, when the same object is pushed up the incline with an initial velocity u, it will move against the gravitational force and friction. As it moves up, the forces acting on it will be:
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting down the incline (since it opposes the motion): f
Step 3: Determine the Net Force Acting on the Object
The net force acting on the object when it is moving up the incline can be expressed as:
Fnet=−mgsinθ−f
Since we already established that f=mgsinθ, we can substitute this into the equation:
Fnet=−mgsinθ−mgsinθ=−2mgsinθ
Step 4: Analyze the Motion of the Object
As the object moves up the incline, it will decelerate due to the net force acting against its motion. Eventually, it will come to a stop when its velocity becomes zero. At this point, all the initial kinetic energy will have been converted into work done against the gravitational and frictional forces.
Step 5: Determine What Happens Next
Once the object comes to a stop, the forces acting on it will again be balanced since the frictional force will equal the gravitational force component acting down the incline. Therefore, the object will not slide down the incline but will remain at rest.
Conclusion
The correct option is that the object stays at rest on the inclined plane and does not slide down.
When the object slides down the inclined plane with uniform velocity, it means that the net force acting on the object is zero. The forces acting on the object are:
- The gravitational force component acting down the incline: Fgravity=mgsinθ
- The frictional force acting up the incline: Ffriction=f
Fgravity=Ffriction
Thus,
mgsinθ=f
Now, when the same object is pushed up the incline with an initial velocity u, it will move against the gravitational force and friction. As it moves up, the forces acting on it will be:
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting down the incline (since it opposes the motion): f
The net force acting on the object when it is moving up the incline can be expressed as:
Fnet=−mgsinθ−f
Since we already established that f=mgsinθ, we can substitute this into the equation:
Fnet=−mgsinθ−mgsinθ=−2mgsinθ
As the object moves up the incline, it will decelerate due to the net force acting against its motion. Eventually, it will come to a stop when its velocity becomes zero. At this point, all the initial kinetic energy will have been converted into work done against the gravitational and frictional forces.
Once the object comes to a stop, the forces acting on it will again be balanced since the frictional force will equal the gravitational force component acting down the incline. Therefore, the object will not slide down the incline but will remain at rest.
The correct option is that the object stays at rest on the inclined plane and does not slide down.
Similar Questions
We use inclined planes to push heavy things up to a certain height.
View SolutionA block slides down a rough inclined plane of slope angle θ with a constnat velocity. It is then projected up the same plane with an intial velocity v the distance travelled by the block up the plane coming to rest is .
View Solution
Knowledge Check
A solid cylinder rolls up an inclined plane of inclination θ with an initial velocity v. How far does the cylinder go up the plane ?
A3v22gsinθBv24gsinθC3v2gsinθD3v24gsinθ
In figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
View SolutionA block kept on a inclined plane slides down the plane with constant velocity when the slope angle of the plane is θ. It is then projected up with an initial velocity u. How far up the incline will it move before coming to rest ? Will it slide down again ?
View SolutionWhen a body rolls without sliding up an inclined plane the frictional force is :
View SolutionAn object in projected up the inclined at the angle shown in the figure with an initial velocity of 30ms−1. The distance x up the incline at which the object lands is
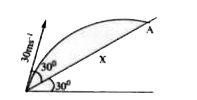
View SolutionIf the angle of inclination of the inclined plane is sin−1(12) when the body just starts sliding find the angle of repose and coefficient of static friction between the body and the inclined plane.
View SolutionStarting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View SolutionA box is placed on an inclined plane and has to be pushed down.The angle of inclination is
View Solution
