A box is placed on an inclined plane and has to be pushed down.The angle of inclination is
equal to angle of repose
more than angle of repose
less than the angle of repose
equal to angle of friction
The correct Answer is:C
To solve the problem of determining the relationship between the angle of inclination of a box on an inclined plane and the angle of repose, we can follow these steps:
1. Understanding Forces on the Box:
- When a box is placed on an inclined plane, it experiences gravitational force (weight) acting downwards. This weight can be resolved into two components:
- One component acting parallel to the incline: Fparallel=mgsinθ
- Another component acting perpendicular to the incline: Fperpendicular=mgcosθ
2. Identifying Normal Force:
- The normal force N acting on the box is equal to the perpendicular component of the weight:
N=mgcosθ
3. Frictional Force:
- The frictional force Ffriction opposing the motion of the box is given by:
Ffriction=μN=μ(mgcosθ)
- Here, μ is the coefficient of friction.
4. Condition for Downward Movement:
- For the box to move downward, the component of gravitational force along the incline must be greater than or equal to the frictional force:
mgsinθ≥μ(mgcosθ)
- Dividing both sides by mg (assuming m≠0):
sinθ≥μcosθ
5. Using the Angle of Repose:
- The angle of repose α is defined as the angle at which the box just begins to slide down the incline. This is given by:
tanα=μ
- Therefore, we can relate sinθ and cosθ to tanα:
sinθ≥tanαcosθ
- This can be rewritten as:
tanθ≥tanα
- Thus, we conclude that:
θ≥α
6. Conclusion:
- Based on the analysis, we find that the angle of inclination θ must be greater than or equal to the angle of repose α for the box to slide down the incline. Therefore, the correct option is that the angle of inclination is more than the angle of repose.
Final Answer:
The angle of inclination is more than the angle of repose.
- When a box is placed on an inclined plane, it experiences gravitational force (weight) acting downwards. This weight can be resolved into two components:
- One component acting parallel to the incline: Fparallel=mgsinθ
- Another component acting perpendicular to the incline: Fperpendicular=mgcosθ
- The normal force N acting on the box is equal to the perpendicular component of the weight:
N=mgcosθ
- The frictional force Ffriction opposing the motion of the box is given by:
Ffriction=μN=μ(mgcosθ)
- Here, μ is the coefficient of friction.
- For the box to move downward, the component of gravitational force along the incline must be greater than or equal to the frictional force:
mgsinθ≥μ(mgcosθ)
- Dividing both sides by mg (assuming m≠0):
sinθ≥μcosθ
- The angle of repose α is defined as the angle at which the box just begins to slide down the incline. This is given by:
tanα=μ
- Therefore, we can relate sinθ and cosθ to tanα:
sinθ≥tanαcosθ
- This can be rewritten as:
tanθ≥tanα
- Thus, we conclude that:
θ≥α
- Based on the analysis, we find that the angle of inclination θ must be greater than or equal to the angle of repose α for the box to slide down the incline. Therefore, the correct option is that the angle of inclination is more than the angle of repose.
The angle of inclination is more than the angle of repose.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 345videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 355videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 328videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A body is placed on an inclined plane and has to be pushed down. The angle made by the normal reaction with the vertical will be:-
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
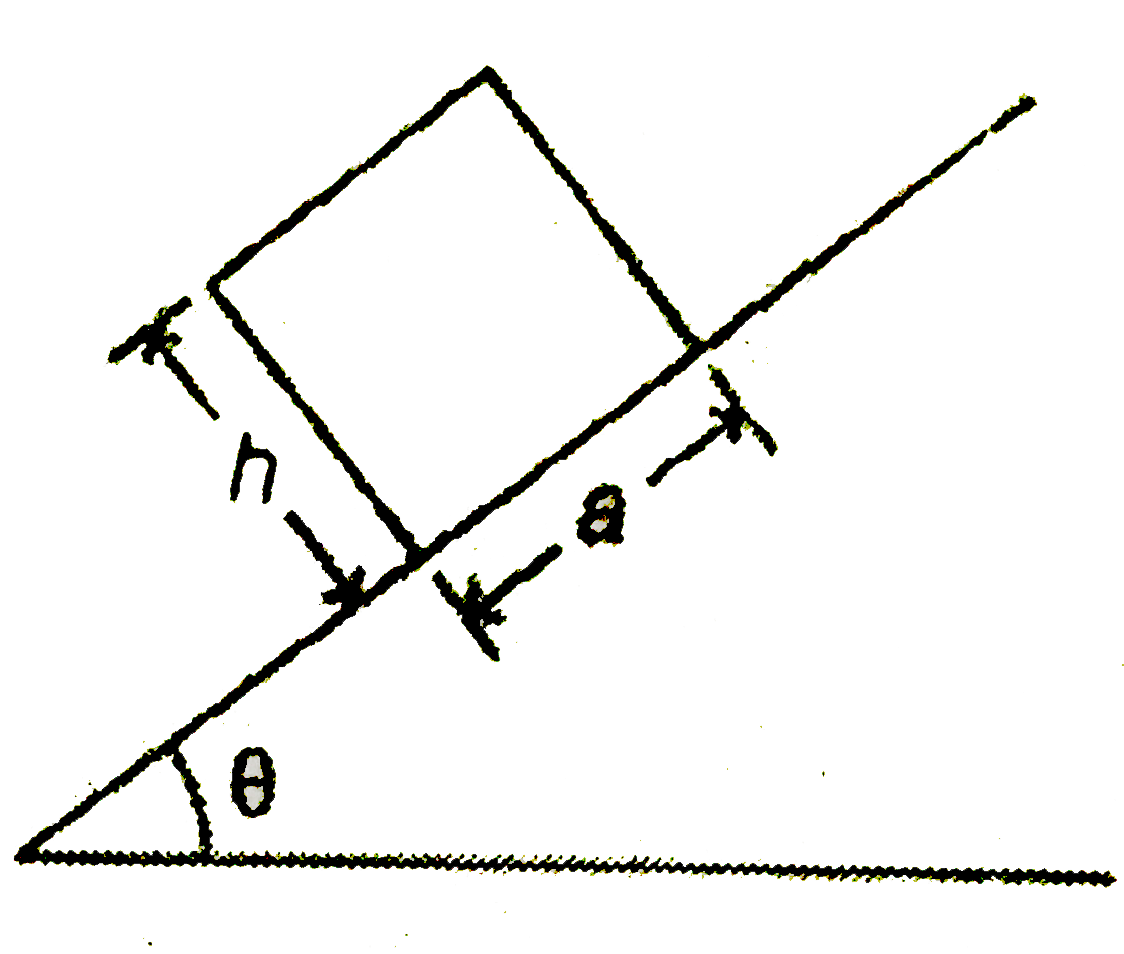 View Solution
View SolutionA wooden block is placed on an inclined plane. The block just begins to slide down when the angle of the inclination is increased to 45°. What is the coefficient of the friction?
View SolutionA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View SolutionA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View SolutionA disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
View SolutionAssertion: A body slides down an inclined plane if the angle of friction is more than the angle of the inclined plane with the horizontal.
Reason : When the angle of inclination is equal to the angle of friction, the component of weight parallel to the plane is just sufficient to overcome the frictional force.View SolutionA body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the contact force between the block and the plane
 View Solution
View SolutionA body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the normal force between the block and the plane is,
 View Solution
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View Solution

