When the displacement of a particle in SHM from the mean position is 4 cm, the force acting on the particle is 6 N. Then the force acting on it when its displacement is 6 cm from the mean positio is
3 N
16 N
8 N
9 N
The correct Answer is:D
To solve the problem step by step, we can use the relationship between force and displacement in Simple Harmonic Motion (SHM). The force acting on a particle in SHM is given by Hooke's Law, which states:
F=−kx
where:
- F is the force,
- k is the spring constant (a measure of stiffness),
- x is the displacement from the mean position.
Step 1: Determine the spring constant k
From the problem, we know that when the displacement x=4 cm, the force F=6 N. We can rearrange the formula to find k:
F=kx
Substituting the known values:
6=k×4
Now, solve for k:
k=64=32N/cm
Step 2: Calculate the force when the displacement is 6 cm
Now, we need to find the force when the displacement x=6 cm. Using the same formula:
F=kx
Substituting k=32 N/cm and x=6 cm:
F=(32)×6
Calculating this gives:
F=3×62=182=9N
Final Answer
The force acting on the particle when its displacement is 6 cm from the mean position is 9 N.
---
- F is the force,
- k is the spring constant (a measure of stiffness),
- x is the displacement from the mean position.
Topper's Solved these Questions
Similar Questions
A body of mass 0.1 kg performing linear SHM experiences a restoring force of 1 N when its displacement from the mean position is 5 cm. Find (i) the force constant (ii) the period of SHM (iii) the acceleration of the body, when its displacement from the mean position is 1 cm./
View SolutionA partical executes SHM on a straigh line path. The amplitude of oscillation is 2cm. When the displacement of the particle from the mean position is 1cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period of SHM, also the ms. velocity and ms. acceleration of SHM.
View Solution
Knowledge Check
The velocity of a particle in simple harmonic motion at displacement y from mean position is
Aω√(a2+y2)Bω√(a2−y2)CwyDω2√(a2+y2)The displacement time curve of a particle is shown in the figure. The external force acting on the particle is :
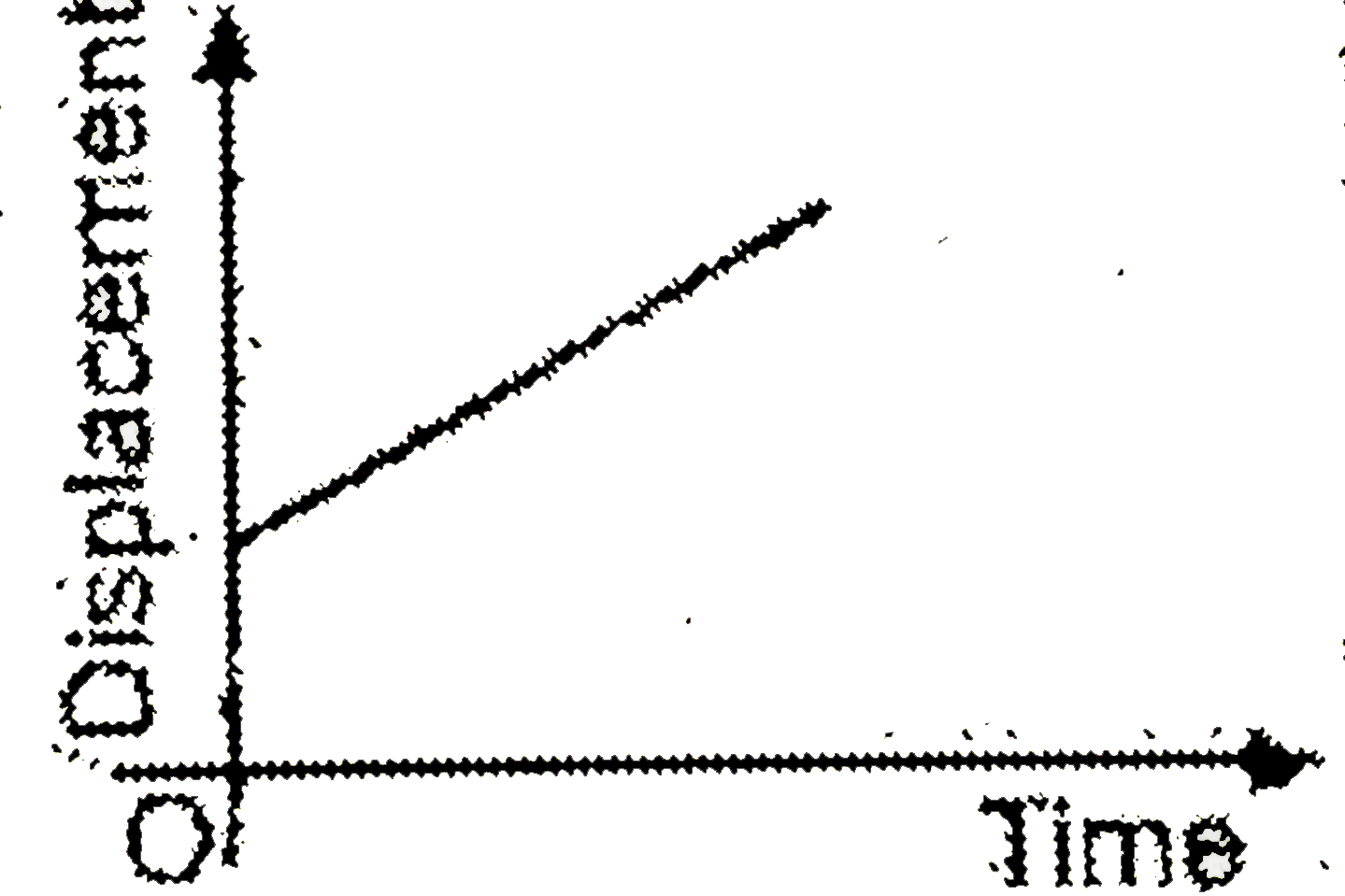 AActing at the beginning part of motionBZeroCNot zeroDNone of these
AActing at the beginning part of motionBZeroCNot zeroDNone of theseA particle performing SHM starts from mean position. The phase of that particle is π/s when it has
Amaximum displacementBmaximum velocityCmaximum energyDmaximum kinetic energy
The positions of maximum displacement of a particle from the mean position of a transverse wave is called ______
View SolutionA body is executing SHM. If the force acting on the body is 6N when the displacement is 2cm, then the force acting on the body at a displacement of 3cm is
View SolutionIn the previous problem, the displacement of the particle from the mean position corresponding to the instant mentioned is
View SolutionThe amplitude of a particle executing SHM is 4 cm. At the mean position, the speed of the particle is 16 cm/s. The distance of the particle from the mean position at which the speed of the particle becomes 8√3 cm/sec will be
View SolutionThe velocity of a particle in simple harmonic motion at displacement y from mean position is
View Solution
