When the force on a object depends on the position of the object, we cannot find the work done by it on the object by simple multiplying the force by the displacement. The reason is that there is no one value for the force-it changes. So, we must find the work in tiny little displacements and then add up all the workk results. We effectively say, "Yes, the force varies over any given tiny little displacement. but the variation is so small we can approximate the force as being constant during the displacements infinitesimal, then our error becomes infinitesimal and the result becomes precise. But, to add an infinite number of work contributions by hand would take us forever, longer than a semester.So we add them up via an integration, which allows us to do all this in minutes (much less than a semester).
Force →F=(3x2N)ˆi+(4N)ˆj, with x in meters, acts on a particle, changing only the kinetic energy of th particle. How much work is done on the particle as it moves from coordinates (2 , 3 m) to 3 m, 0 m)? Does the speed of the particle increase, decrease, or remain the same?
KEY IDEA
The force is a variable force because its x component depends on the value of x. Thus, we cannot use Eqs. 8-7 and 8-8 to find the work done. Instead, we must use Eq. 8-36 to integrate the force.
Calculation: We set up two integrals, one along each axis:
W=∫323x2dx+∫034dy=3∫32x2dx+4∫03dy
=3[12x3]32+4[y]03=[33−23]+4[0−3]
=7.0J.
The positive result means that energy is transferred to the particle by force →F. Thus, the kinetic energy of the particle increases and, because =1/2mv2, its speed must also increase. If the work had come out negative, the kinetic energy and speed would have decreased.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
Knowledge Check
Work done by a force on an object is zero, if
Athe force is always perpenicular to its accelerationBthe object is stationary but the point of application of the force moves on the objectCthe force is always perpendicular to its velocityDthe object moves in such a way that the point of application of the force remains fixed
How is work done by a force measured when the force :
is in the direction of displacement.
View SolutionA force of 7N acts on an object. The displacement is, say 8m, in the direction of the force, Let us take it that the force acts on the object throughout the displacement. What is the work done in this case ?
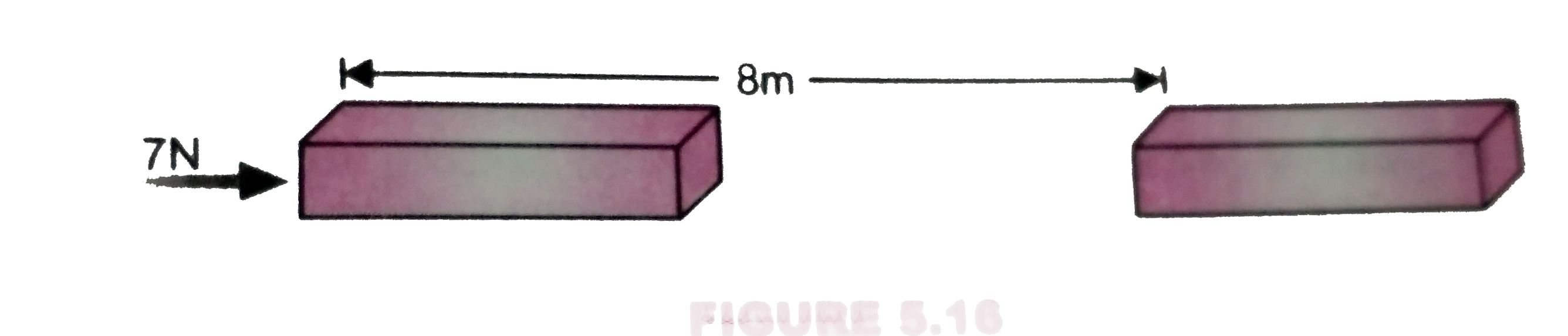
View SolutionA force of 7N acts on an object. The displacement is, say 8m, in the direction of the force, Let us take it that the force acts on the object throughout the displacement. What is the work done in this case ?

View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
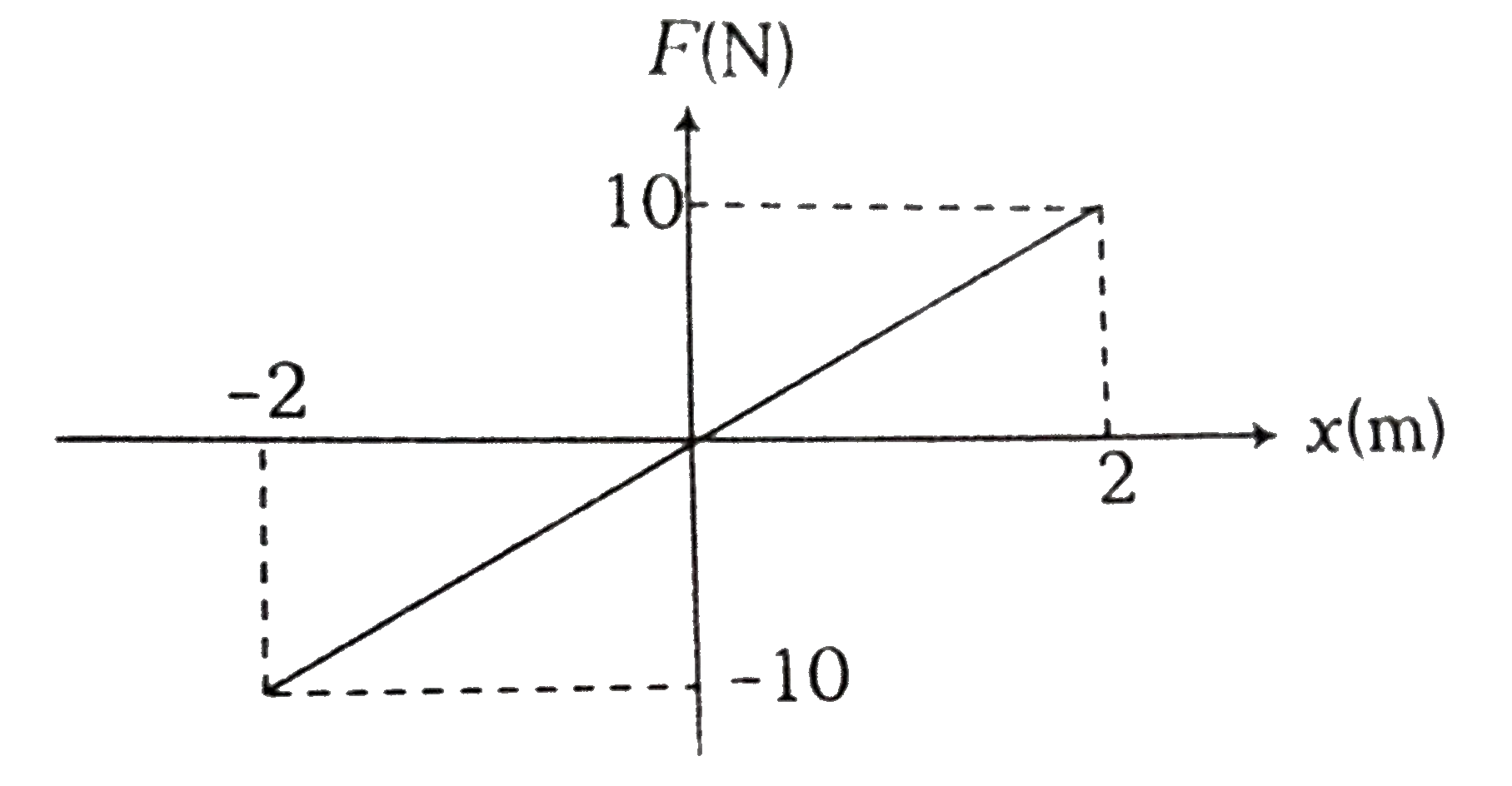
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionWhat is the work done by a force when the force is:
Normal to the displacement produced.
View SolutionWrite an expression for the work done when a force is acting on an object in the direction of its displacement.
View Solution
