When the polariser and analyser are in the crossed position the intensity of the out coming light is
maximum
minimum
it depends on the type of analyser
partially maximum
The correct Answer is:B
To determine the intensity of light when the polarizer and analyzer are in the crossed position, we can follow these steps:
1. Understanding Polarization:
- Light can be polarized using a polarizer, which allows only light waves oscillating in a particular direction to pass through.
2. Position of Polarizer and Analyzer:
- The polarizer and analyzer are two optical devices that can be oriented at various angles to each other. When they are in the "crossed position," they are oriented at 90 degrees to each other.
3. Using Malus's Law:
- Malus's Law states that when polarized light passes through a polarizer, the intensity of the transmitted light (I) is given by:
I=I0cos2(θ)
- Here, I0 is the intensity of the incoming light, and θ is the angle between the light's polarization direction and the axis of the polarizer.
4. Applying the Crossed Position:
- In the crossed position, the angle θ between the polarizer and analyzer is 90 degrees.
- Therefore, we substitute θ=90∘ into Malus's Law:
I=I0cos2(90∘)
5. Calculating the Intensity:
- We know that cos(90∘)=0.
- Thus, substituting this value:
I=I0⋅02=0
6. Conclusion:
- The intensity of the light when the polarizer and analyzer are in the crossed position is 0. This means no light passes through.
Final Answer:
The intensity of the outgoing light when the polarizer and analyzer are in the crossed position is 0.
- Light can be polarized using a polarizer, which allows only light waves oscillating in a particular direction to pass through.
- The polarizer and analyzer are two optical devices that can be oriented at various angles to each other. When they are in the "crossed position," they are oriented at 90 degrees to each other.
- Malus's Law states that when polarized light passes through a polarizer, the intensity of the transmitted light (I) is given by:
I=I0cos2(θ)
- Here, I0 is the intensity of the incoming light, and θ is the angle between the light's polarization direction and the axis of the polarizer.
- In the crossed position, the angle θ between the polarizer and analyzer is 90 degrees.
- Therefore, we substitute θ=90∘ into Malus's Law:
I=I0cos2(90∘)
- We know that cos(90∘)=0.
- Thus, substituting this value:
I=I0⋅02=0
- The intensity of the light when the polarizer and analyzer are in the crossed position is 0. This means no light passes through.
The intensity of the outgoing light when the polarizer and analyzer are in the crossed position is 0.
Topper's Solved these Questions
Similar Questions
When a polariser and analyser have their axes inclined to one another at 30∘ , the amount of light transmitted is 5 SI units. What is the maximum intensity of light transmitted and at what angle between the two?
View SolutionA unpolarised light is passed through 3 polarisers. If the second polariser is at an angle 30∘ with the first and the third polariser is at an angle 60∘ with the second. Find the final intensity of the light passed through this combination in initial intensity was I.
View Solution
Knowledge Check
- Question 1 - Select One
The polariser and analyser are inclined to each other at 60∘. The intensity of polarised light emerging from polariser is I. The intensity of the unpolarised light incident on the polariser is
AIB8IC4ID2I - Question 2 - Select One
When a plane polarised light is passed through an analyser and analyser is rotated through 90∘, the intensity of the emerging light
AVaries between a maximum and minimumBBecome zeroCDoes not varyDVaries between a maximum and zero - Question 3 - Select One
If θ is the angle between the transmission axes of the polarizer and the analyser and I0 be the intensity of the polarized light incident on the analyser, then Intensity of transmitted light through analyser would be
A(I0cosθ)2B√2I0cos2θCI0√2cos2θDI0cos2θ
The orientation between a polariser and an analyser is such that the intensity of transmitted light is maximum. On rotating the analyser through 60∘, what fraction of maximum light will be transmitted?
View SolutionIf the angle between the pass axis of polariser and the analyser is 45∘, write the ratio of the intensities of original light and the transmitted light after passing through the analyser.
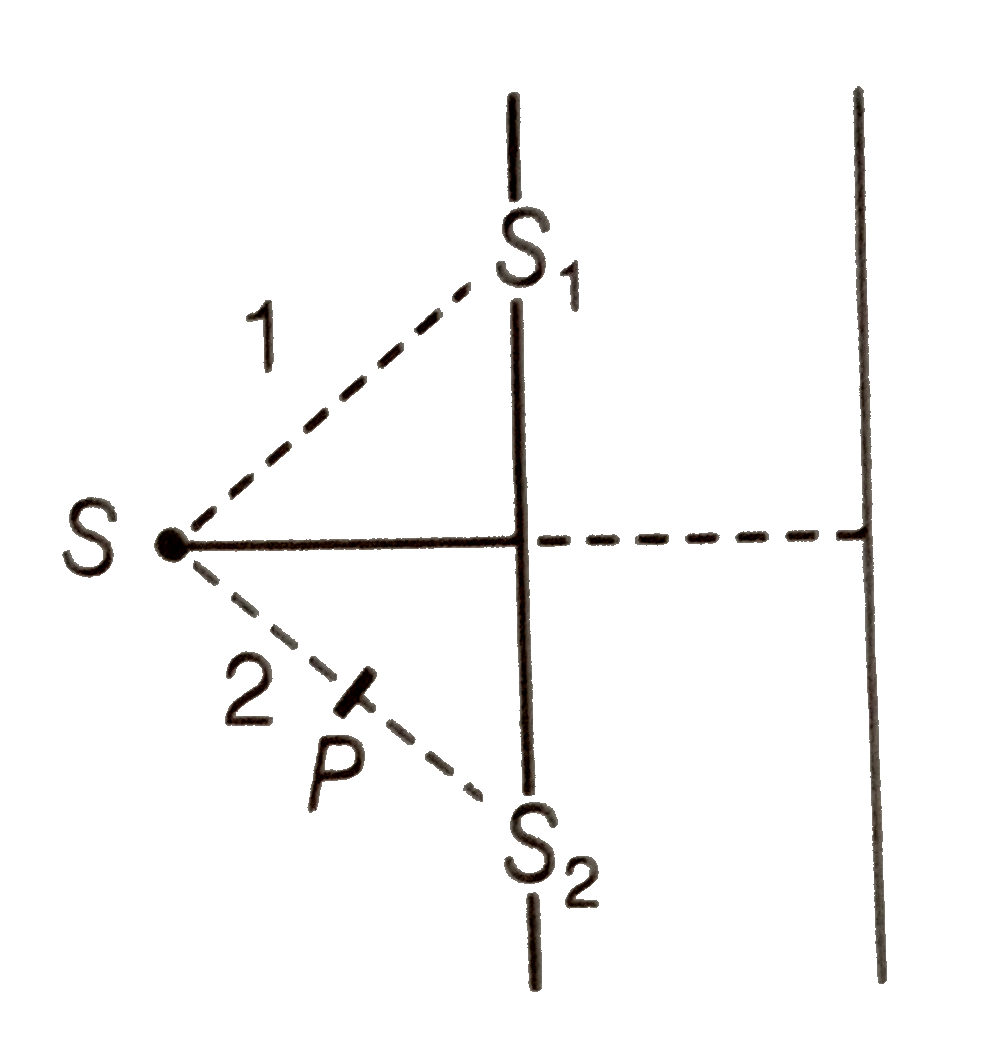
View SolutionFigure shown a two slit arrangement with a source which emits unpolarised light. P is a polariser with axis whose direction is not given. If I0 is the intensity of the principal maxima when no polariser is present, calculte in the present case, the intensity of the principal maxima as well as the first minima.
 View Solution
View SolutionPolarods are used to control the intensity of light coming through windows of
View SolutionUnpolarised light of internsity 32Wm−2 passes through three polarisers such that the transmission axis of the last polariser is crossed with the first. If the intensity of emerging light is 2Wm−2, the angle between the transmission axes o the first two polarisers is
View Solution

