When two resistors are connected in series with a cell of emf 2 V and negligible internal resistance, a current of $\frac{2}{5}$ A flows in the circuit. When the resistors are connected in parallel the main current is $\frac{5}{3} A$ . Calculate the resistances.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to find the resistances $R_{1}$ and $R_{2}$ given the conditions of the circuit.
1. Understanding the Series Connection:
When two resistors $R_{1}$ and $R_{2}$ are connected in series with a cell of EMF $V = 2 V$ , the total resistance $R_{s}$ is given by:
$R_{s} = R_{1} + R_{2}$
The current flowing through the circuit is $I_{s} = \frac{2}{5} A$ .
2. Using Ohm's Law:
According to Ohm's Law, $V = I \cdot R$ . Therefore, we can write:
$V = I_{s} \cdot R_{s}$
Substituting the known values:
$2 = (\frac{2}{5}) \cdot (R_{1} + R_{2})$
3. Solving for $R_{1} + R_{2}$ :
Rearranging the equation gives:
$R_{1} + R_{2} = \frac{2}{\frac{2}{5}} = 5 Ω (Equation 1)$
4. Understanding the Parallel Connection:
When the same resistors are connected in parallel, the equivalent resistance $R_{p}$ is given by:
$\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$
The total current flowing through the circuit in this case is $I_{p} = \frac{5}{3} A$ .
5. Using Ohm's Law for Parallel Connection:
Again using Ohm's Law:
$V = I_{p} \cdot R_{p}$
Substituting the known values:
$2 = (\frac{5}{3}) \cdot R_{p}$
6. Solving for $R_{p}$ :
Rearranging gives:
$R_{p} = \frac{2}{\frac{5}{3}} = \frac{6}{5} Ω$
Using the formula for parallel resistances:
$\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$
We can substitute $R_{p}$ :
$\frac{1}{\frac{6}{5}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$
This simplifies to:
$\frac{5}{6} = \frac{1}{R_{1}} + \frac{1}{R_{2}} (Equation 2)$
7. Setting Up the Equations:
We now have two equations:
- $R_{1} + R_{2} = 5$ (Equation 1)
- $\frac{1}{R_{1}} + \frac{1}{R_{2}} = \frac{5}{6}$ (Equation 2)
8. Substituting Equation 1 into Equation 2:
From Equation 1, we can express $R_{2}$ as:
$R_{2} = 5 - R_{1}$
Substituting into Equation 2:
$\frac{1}{R_{1}} + \frac{1}{5 - R_{1}} = \frac{5}{6}$
9. Clearing the Denominators:
Multiplying through by $6 R_{1} (5 - R_{1})$ :
$6 (5 - R_{1}) + 6 R_{1} = 5 R_{1} (5 - R_{1})$
Simplifying gives:
$30 - 6 R_{1} + 6 R_{1} = 25 - 5 R_{1}^{2}$
Thus:
$5 R_{1}^{2} - 25 + 30 = 0 \Rightarrow 5 R_{1}^{2} - 5 = 0$
10. Factoring the Quadratic:
Dividing through by 5:
$R_{1}^{2} - 1 = 0 \Rightarrow (R_{1} - 1) (R_{1} + 1) = 0$
So, $R_{1} = 1 Ω$ or $R_{1} = - 1 Ω$ (not possible).
11. Finding $R_{2}$ :
If $R_{1} = 1 Ω$ , then:
$R_{2} = 5 - 1 = 4 Ω$
Final Answer:
Thus, the resistances are:
$R_{1} = 1 Ω, R_{2} = 4 Ω$

Updated on:18/9/2024

When resistors are connected in series, then net resistance_____
Aincreases
Bdecreases
Cremains same
DNone of these
Shows a network of eight resistors battery of resistance $R (= 2 Ω)$ connected in a $3 V$ battery of negligible internal resistance. The current $I$ in the circuit is

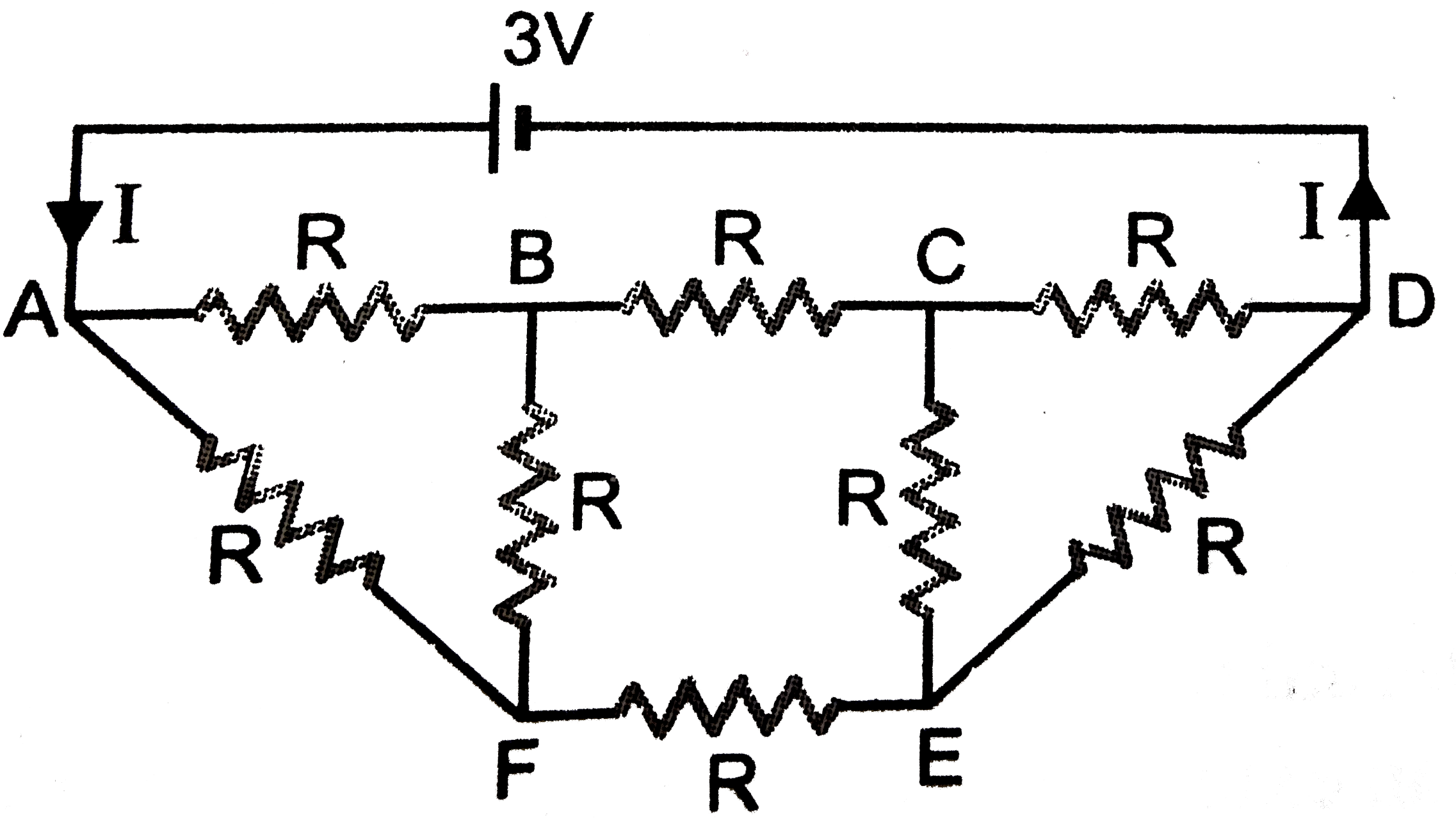A $0.25 A$
B $0.50 A$
C $0.75 A$
D $1.0 A$
Three similar cells, each of emf 2 V and internal resistance $r Ω$ send the same current through an external resistance of $2 Ω$ , when connected in series or in parallel. The strength of the current flowing through the external resistance is
A $1 A$
B $1.5 A$
C $2 A$
D $0.75 A$