When we apply a force on a wall of infinite mass but the wall remains at rest, have we done any work on the wall? Does the wall do work on us?
To solve the question of whether work is done on a wall of infinite mass when we apply a force to it, we can follow these steps:
1. Understanding Work Done:
Work done (W) is defined as the product of the force (F) applied and the displacement (d) in the direction of the force. Mathematically, it is expressed as:
W=F⋅d⋅cos(θ)
where θ is the angle between the force and the direction of displacement.
2. Analyzing the Situation:
In this scenario, we are applying a force on a wall with infinite mass. The wall does not move, which means the displacement (d) of the wall is zero.
3. Calculating Work Done on the Wall:
Since the wall remains at rest and does not move, the displacement d=0. Therefore, substituting this into the work formula:
W=F⋅0⋅cos(θ)=0
This indicates that no work is done on the wall.
4. Considering the Angle:
The angle θ between the applied force and the direction of displacement is 90 degrees (since we are pushing against the wall). The cosine of 90 degrees is zero:
cos(90∘)=0
This further confirms that the work done is zero.
5. Work Done by the Wall:
Now, we need to consider if the wall does any work on us. For the wall to do work on us, it would need to exert a force that causes displacement in our direction. However, since the wall is also at rest and does not move, the displacement of us is also zero.
6. Conclusion:
Since both the wall does not move and we do not move, the work done by the wall on us is also zero:
Wwall=0
Final Answer:
- No, we have not done any work on the wall.
- No, the wall does not do any work on us.
Work done (W) is defined as the product of the force (F) applied and the displacement (d) in the direction of the force. Mathematically, it is expressed as:
W=F⋅d⋅cos(θ)
where θ is the angle between the force and the direction of displacement.
In this scenario, we are applying a force on a wall with infinite mass. The wall does not move, which means the displacement (d) of the wall is zero.
Since the wall remains at rest and does not move, the displacement d=0. Therefore, substituting this into the work formula:
W=F⋅0⋅cos(θ)=0
This indicates that no work is done on the wall.
The angle θ between the applied force and the direction of displacement is 90 degrees (since we are pushing against the wall). The cosine of 90 degrees is zero:
cos(90∘)=0
This further confirms that the work done is zero.
Now, we need to consider if the wall does any work on us. For the wall to do work on us, it would need to exert a force that causes displacement in our direction. However, since the wall is also at rest and does not move, the displacement of us is also zero.
Since both the wall does not move and we do not move, the work done by the wall on us is also zero:
Wwall=0
- No, we have not done any work on the wall.
- No, the wall does not do any work on us.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzero
When do we say that work is done ?
View SolutionA particle is in its ground state in a unidimensional potential well with infinitely high walls. Find the force with which the particle acts on the walls. Do the calculations for an electron in a well 10−10 m wide.
View SolutionIf 15 workers can build a wall in 48 hours, how many workers will berequired to do the same work in 30 hours?
View SolutionA block of mass 5kg is held against a wall with a force of 100N. as shown om figure. It is moved horizontally slowly by applying a force parallel to the wall. Then the fricational force on the block due to wall is 25x newton. Find x. (Given μ=0.5 and g=10m/sec2)
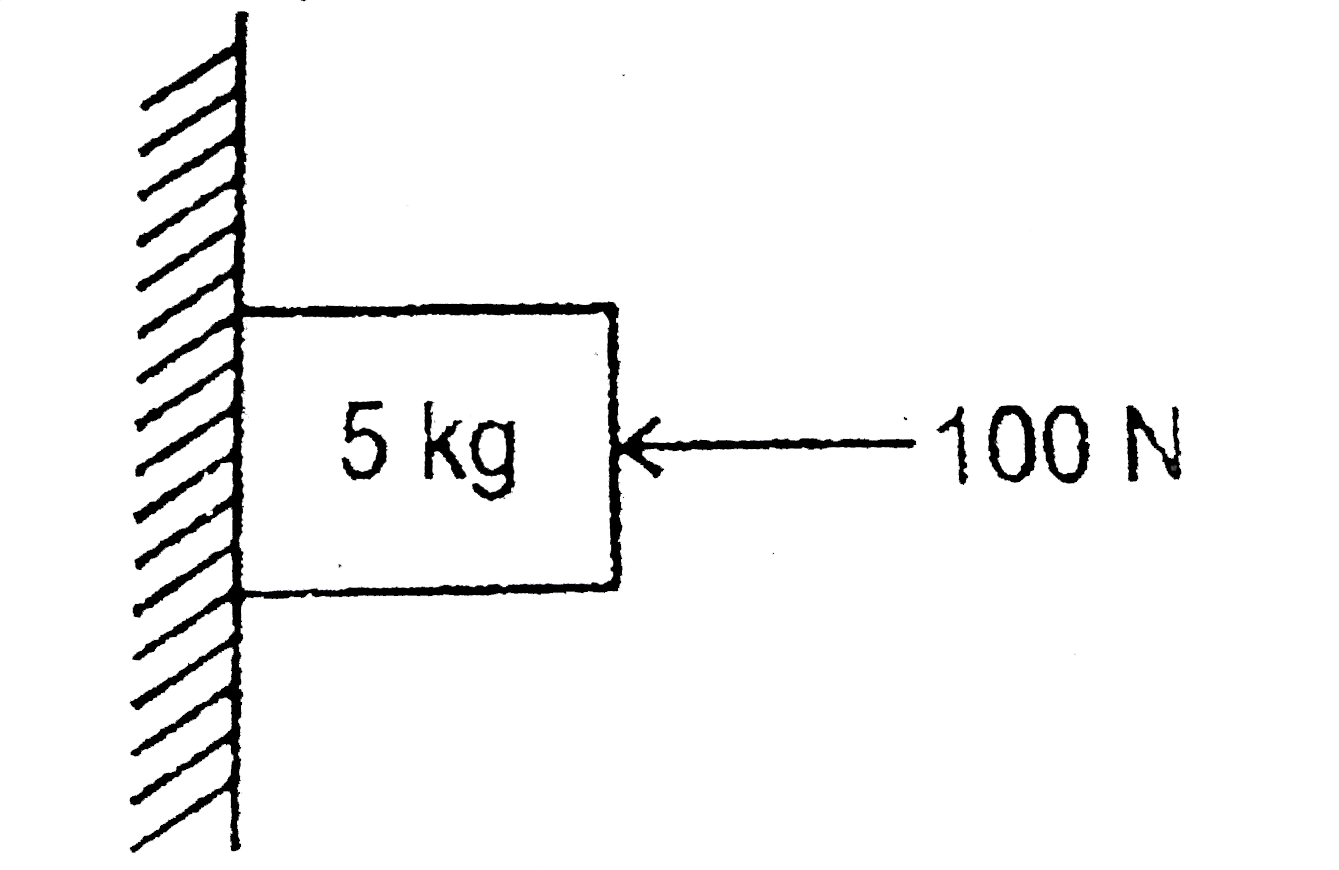
View Solution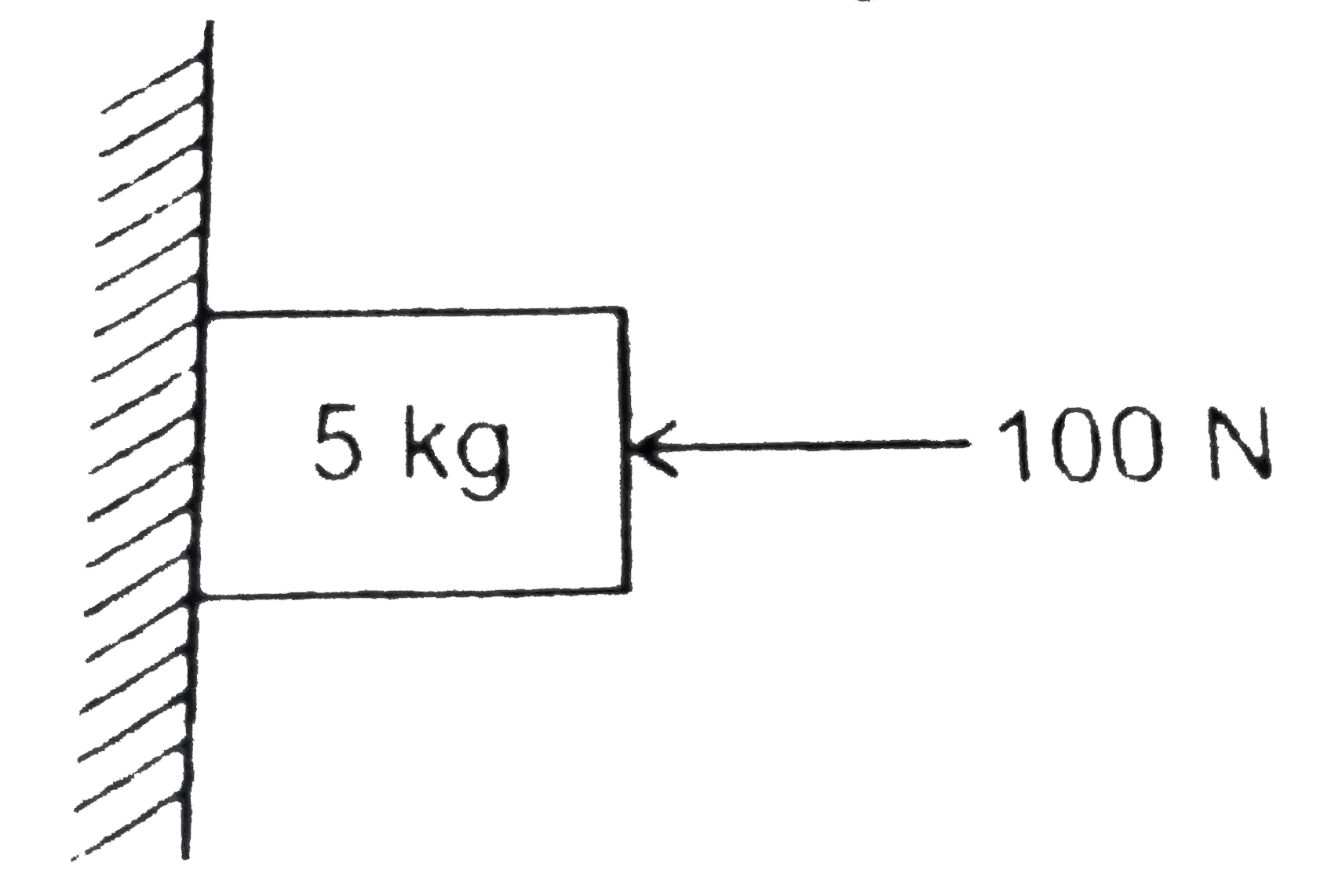
A block of mass 5 kg is held against a wall with a force of 100 N. as shown in figure. It is moved horizontally slowly by applying a force parallel to the wall. Thent he frictional force on the block due to wall is 25x newton find x. (given μ=0.5 and g=10msec2
View SolutionIf 56 workers can build a wall in 180 hours, how many workers will be required to do the same work in 70 hours ?
View SolutionA block of mass 'M' is pressed against a wall with a horizontal force F. Then
a) it will slide down if the wall is smooth
b) frictional force may balance the weight if the wall is rough
c) Normal reaction is equal to weight of the block
d) Normal reaction is zero if the wall is smooth
View Solution
