Which of the following curves represents the variation of impedance with frequency in series circuit?
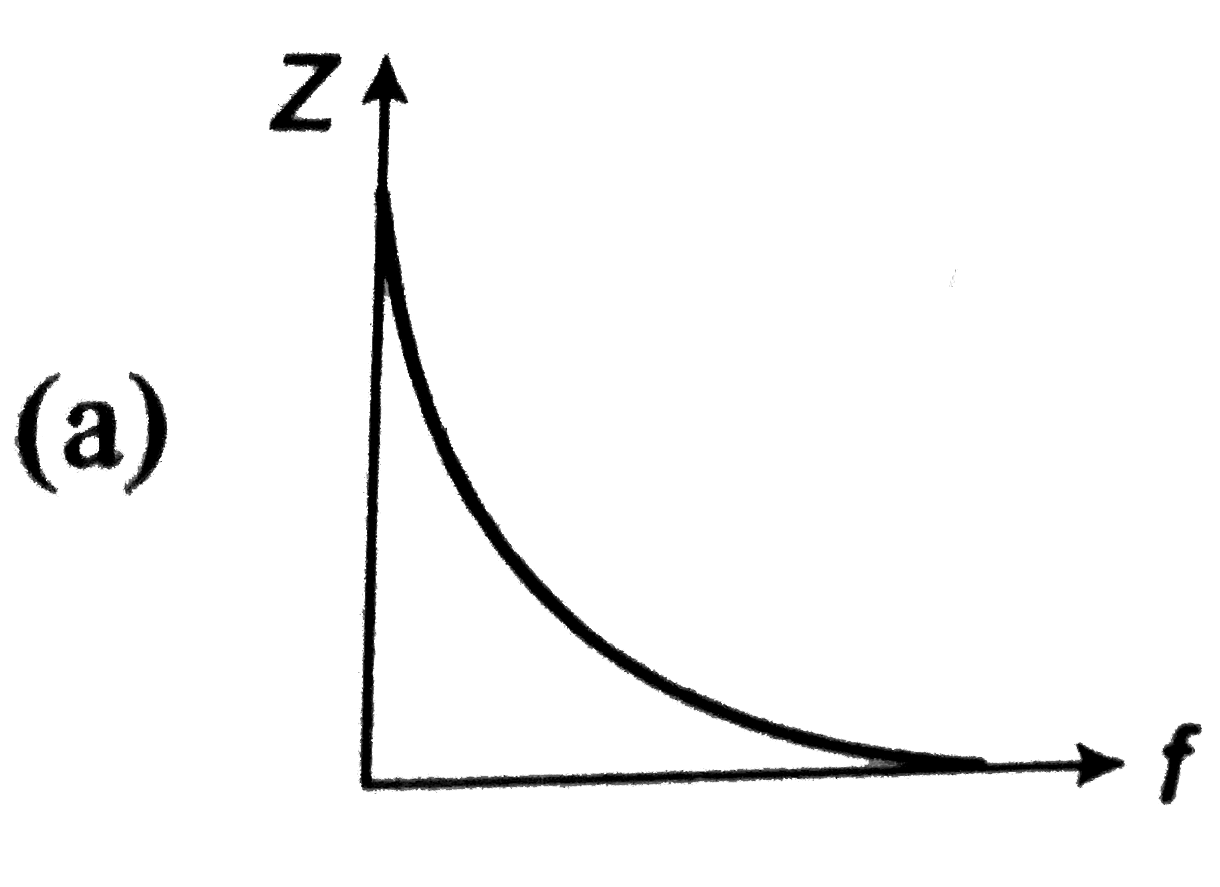

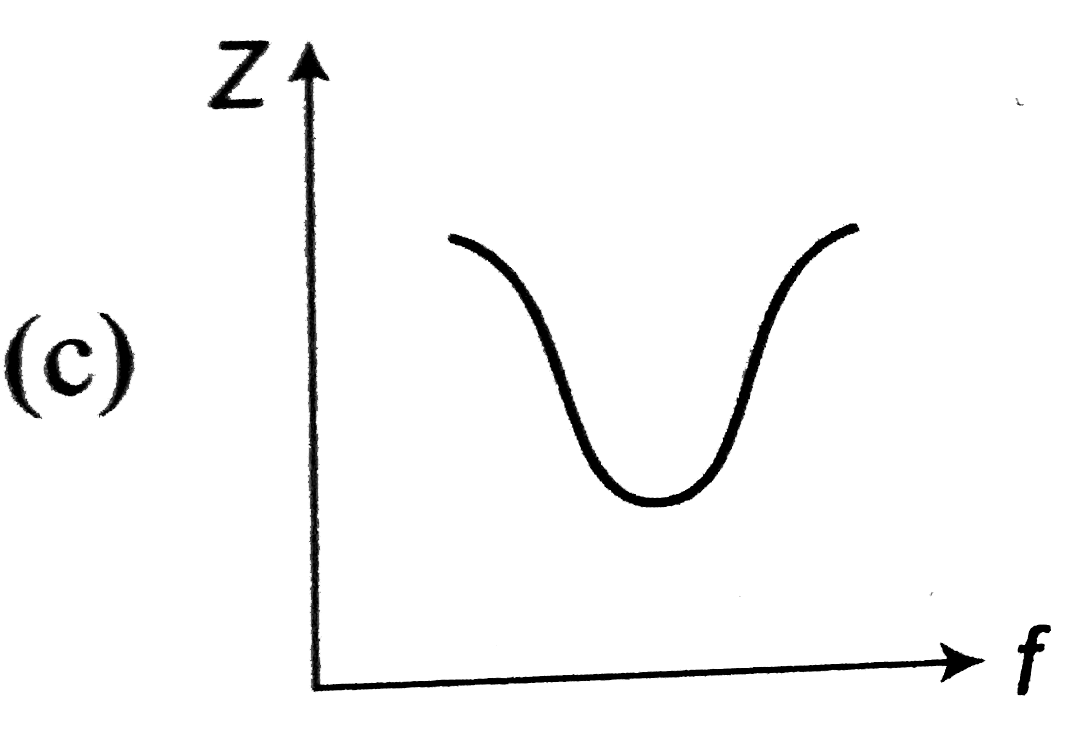
The correct Answer is:C
To determine the variation of impedance Z with frequency f in a series LCR circuit, we can follow these steps:
Step 1: Understand the Impedance Formula
The impedance Z of a series LCR circuit is given by the formula:
Z=√R2+(XL−XC)2
where:
- R is the resistance,
- XL=ωL=2πfL is the inductive reactance,
- XC=1ωC=12πfC is the capacitive reactance.
Step 2: Express Impedance in Terms of Frequency
Substituting the expressions for XL and XC into the impedance formula, we have:
Z=√R2+(2πfL−12πfC)2
Step 3: Analyze the Behavior at Different Frequencies
1. At f=0:
- XL=0
- XC approaches infinity.
- Therefore, Z approaches infinity.
2. At Resonant Frequency f=fR:
- At resonance, XL=XC which implies 2πfRL=12πfRC.
- Thus, Z=R (minimum impedance).
3. At f→∞:
- XL approaches infinity.
- XC approaches 0.
- Therefore, Z approaches infinity.
Step 4: Sketch the Impedance vs Frequency Curve
- Starting from infinity at f=0, the impedance decreases as frequency increases until it reaches a minimum value R at the resonant frequency fR.
- After the resonant frequency, as frequency continues to increase, the impedance increases again towards infinity.
Step 5: Identify the Correct Curve
From the analysis, the curve that represents this behavior will start from infinity, decrease to a minimum at the resonant frequency, and then increase back to infinity. This corresponds to a U-shaped curve.
Conclusion
The correct option that represents the variation of impedance Z with frequency f in a series LCR circuit is option C.
---
The impedance Z of a series LCR circuit is given by the formula:
Z=√R2+(XL−XC)2
where:
- R is the resistance,
- XL=ωL=2πfL is the inductive reactance,
- XC=1ωC=12πfC is the capacitive reactance.
Substituting the expressions for XL and XC into the impedance formula, we have:
Z=√R2+(2πfL−12πfC)2
1. At f=0:
- XL=0
- XC approaches infinity.
- Therefore, Z approaches infinity.
- At resonance, XL=XC which implies 2πfRL=12πfRC.
- Thus, Z=R (minimum impedance).
- XL approaches infinity.
- XC approaches 0.
- Therefore, Z approaches infinity.
- Starting from infinity at f=0, the impedance decreases as frequency increases until it reaches a minimum value R at the resonant frequency fR.
- After the resonant frequency, as frequency continues to increase, the impedance increases again towards infinity.
From the analysis, the curve that represents this behavior will start from infinity, decrease to a minimum at the resonant frequency, and then increase back to infinity. This corresponds to a U-shaped curve.
The correct option that represents the variation of impedance Z with frequency f in a series LCR circuit is option C.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ALTERNATING CURRENTEXERCISE - Power In Ac Circuits21videos
ALTERNATING CURRENT
- BOOK - A2ZCHAPTER - ALTERNATING CURRENTEXERCISE - Problems Based On Mixed Concepts40videos
ALTERNATING CURRENT
- BOOK - A2ZCHAPTER - ALTERNATING CURRENTEXERCISE - Connected With Ac42videos
ALTERNATING CURRENT
- BOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test30videos
ATOMIC PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following curves represents the variation of impedance (Z) with frequency f in series LCR circuit?
A B
B C
C D
D
- Question 2 - Select One
In a series LCR circuit
 Athe voltage VL across the inductance leads the current in the circuit by a phase angle of π/2Bthe voltage VC across the capacitance lags behind the current by a phase angle of π/2Cthe voltage VR across the resistance is in phase with the currentDthe voltage across sereis combination of L, C and R is V=VL+VC+VR
Athe voltage VL across the inductance leads the current in the circuit by a phase angle of π/2Bthe voltage VC across the capacitance lags behind the current by a phase angle of π/2Cthe voltage VR across the resistance is in phase with the currentDthe voltage across sereis combination of L, C and R is V=VL+VC+VR - Question 3 - Select One
Which of the following graphs represent the variation of current(I) with frequency (f) in an AC circuit containing a pure capacitor?
A B
B C
C D
D
what is resonance in series LCR circuit ?
View SolutionSketch a graph that shows change in reactance with frequency of a series LCR circuit.
View SolutionAn a.c. source of variable angular frequency o is connected to an LCR series circuit. Which one of the following graphs correctly represents variation of impedance Zof a.c. circuit with angular frequency ω?
View SolutionAt resonance frequency the impedance in series LCR circuit is
View SolutionThe given curve represents the variation of temperatue as a function of volume for one mole of an ideal gas. Which of the following curves best represents the variation of pressure as a function of volume ?
(##DCP_V03_C20_E01_099_Q01##).View Solution

