Which quantity is conserved during the oscillation of a simple pendulum ?

Video Solution

Answer

Step by step video & image solution for Which quantity is conserved during the oscillation of a simple pendulum ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

BOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Problems for self practice
67videos
OSCILLATIONS
BOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice
66videos
MOTION IN ONE DIMENSION
BOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise
49videos
Physical world

Knowledge Check

Question 1 - Select One
A graph is drawn between the displacement and time taken for the oscillations of a simple pendulum.find the no of oscillation?

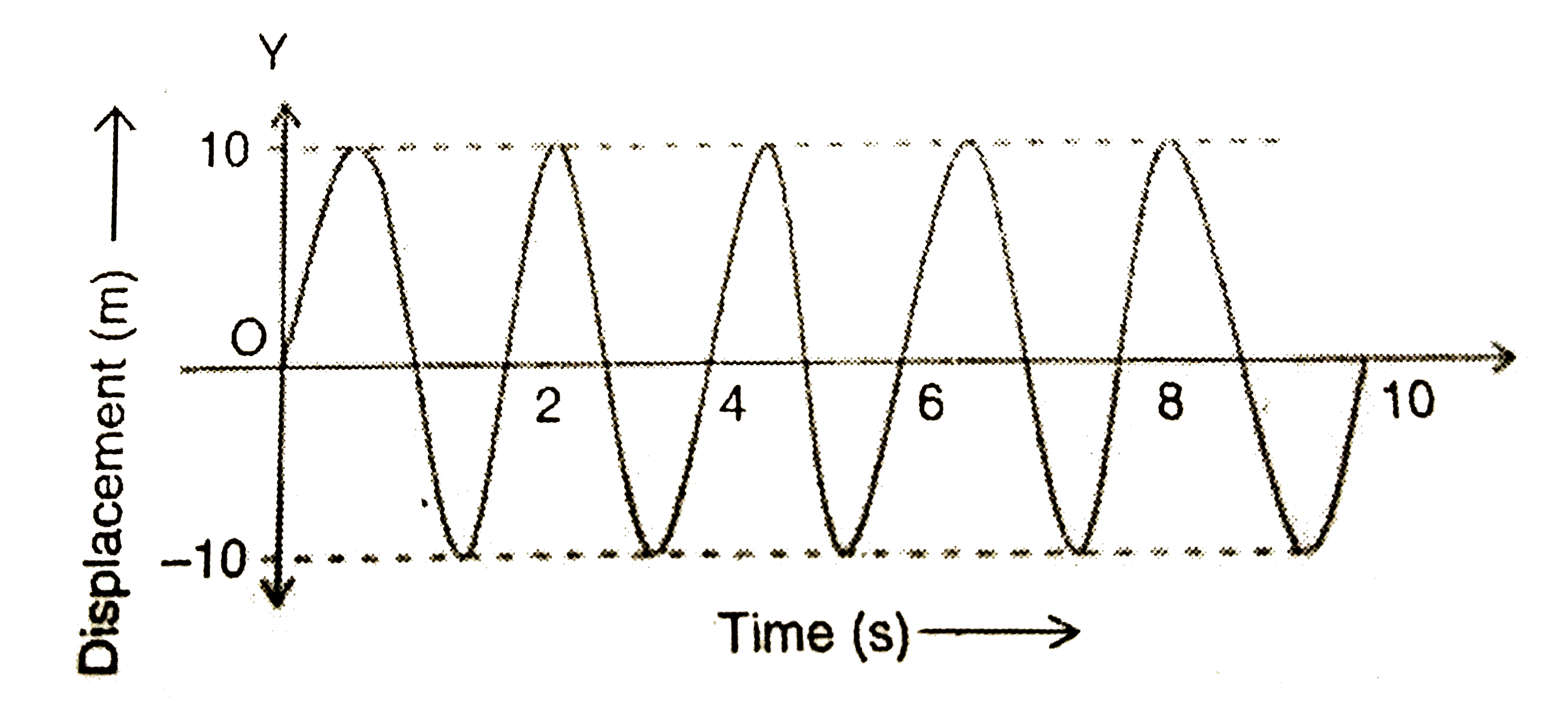A $4^{\frac{1}{2}}$
B5
C6
D $2^{\frac{1}{2}}$
Question 2 - Select One
A graph is drawn between the displacement and time taken for the oscillations of a simple pendulum.find the no of oscillation?

A0.5
B2
C50
D100
Question 3 - Select One
The time taken to complete 100 oscillations is ______ s.

A100
B200
C50
D25