Why does a swinging simple pendulum eventually stop ?
Due to friction between air and bob, the amplitude of simple pendulum goes on decreasing and eventually it comes to rest.
Topper's Solved these Questions
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( LONG ANSWER QUESTIONS )
12 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( NUMERICAL PROBLEMS )
40 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( VERY SHORT ANSWER QUESTIONS )
28 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
24 Videos
- PROPERTIES OF MATTERBOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (NUMERICAL PROBLEMS)
56 Videos
Similar Questions
Knowledge Check
For a simple pendulum the graph between length and time period will be
A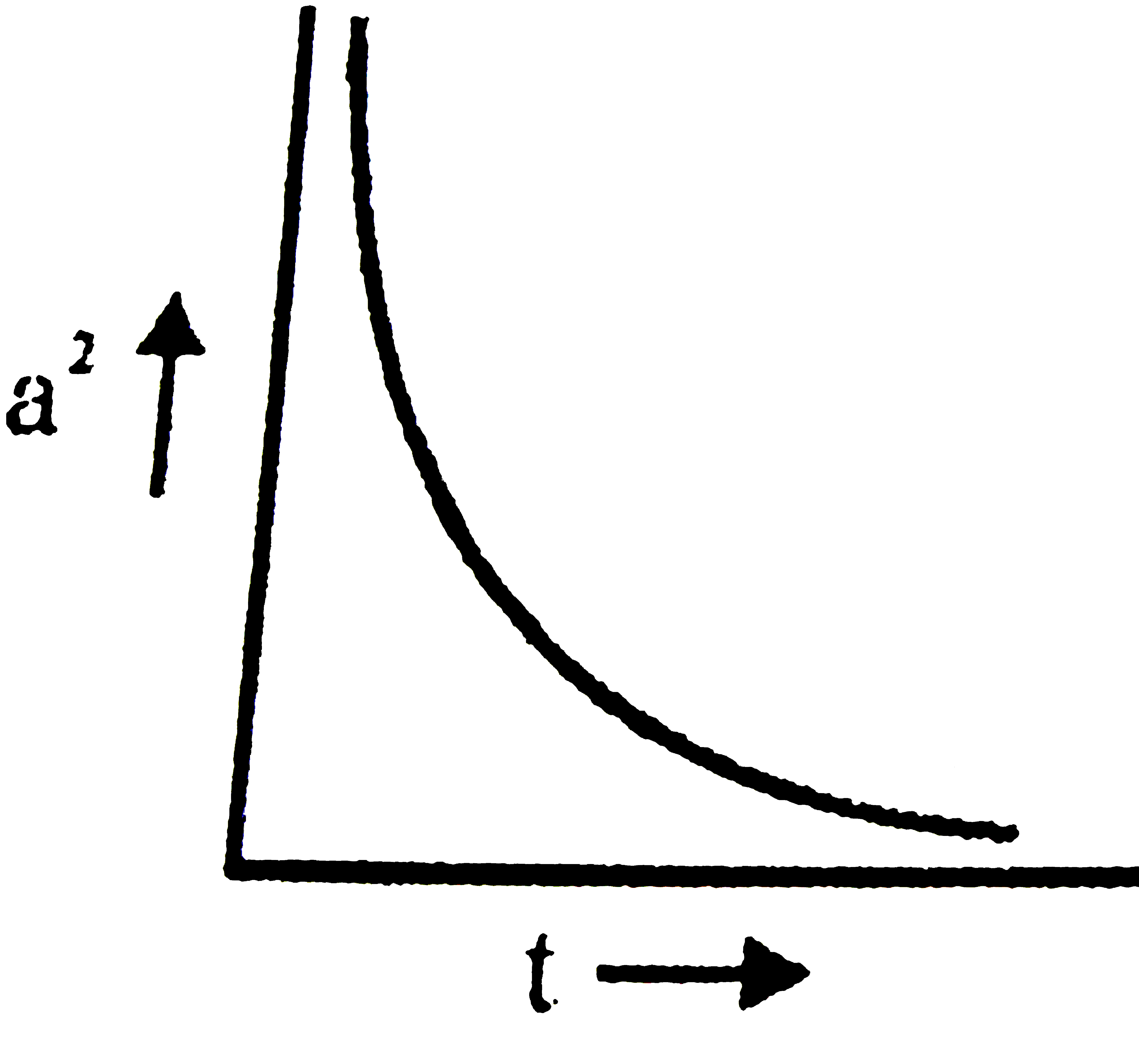 B
B C
C D
D
In an experiment , to find the loss of energy with respect to time in case of swinging simple pendulum , the graph between (amplitude)2 and time is
A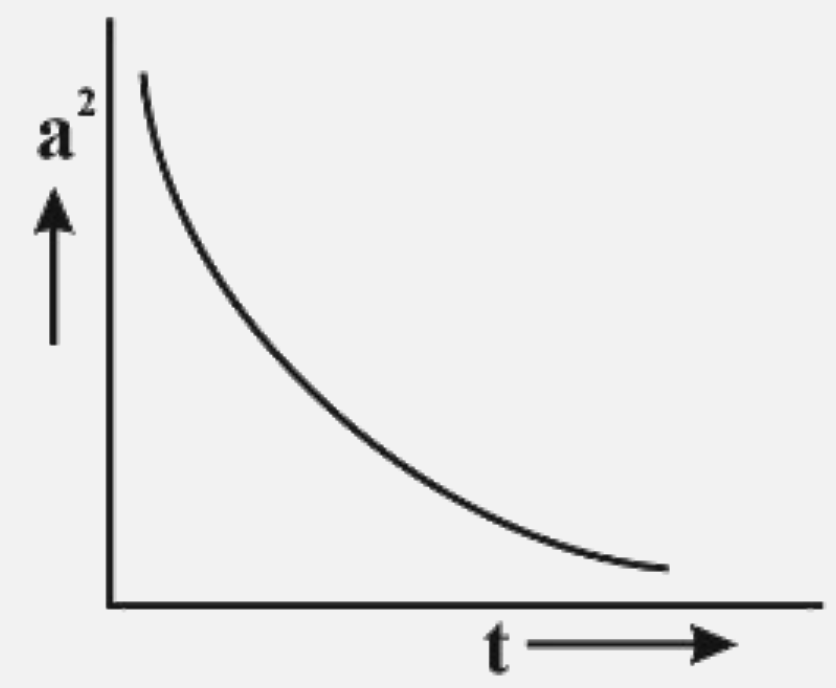 B
B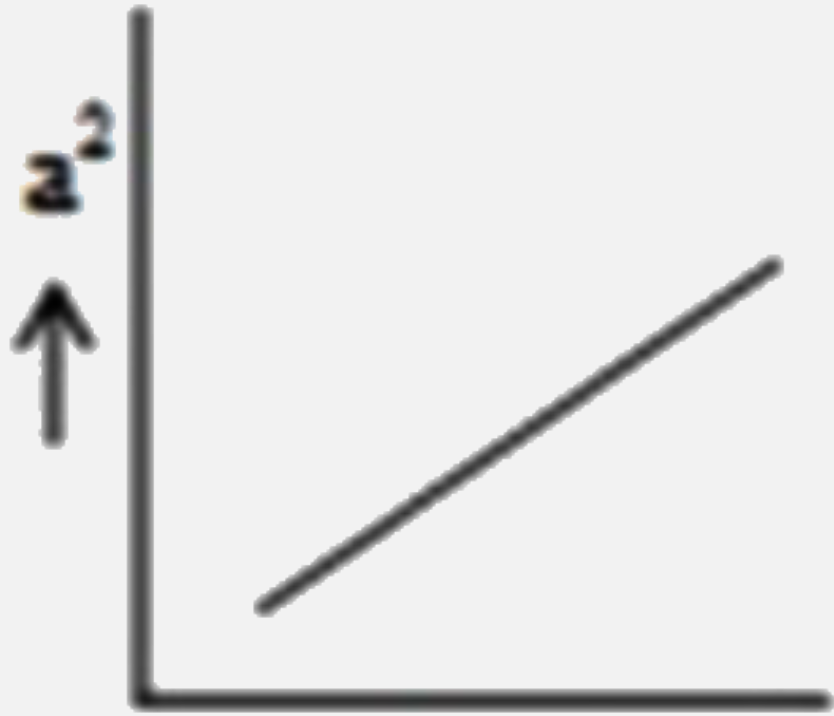 C
C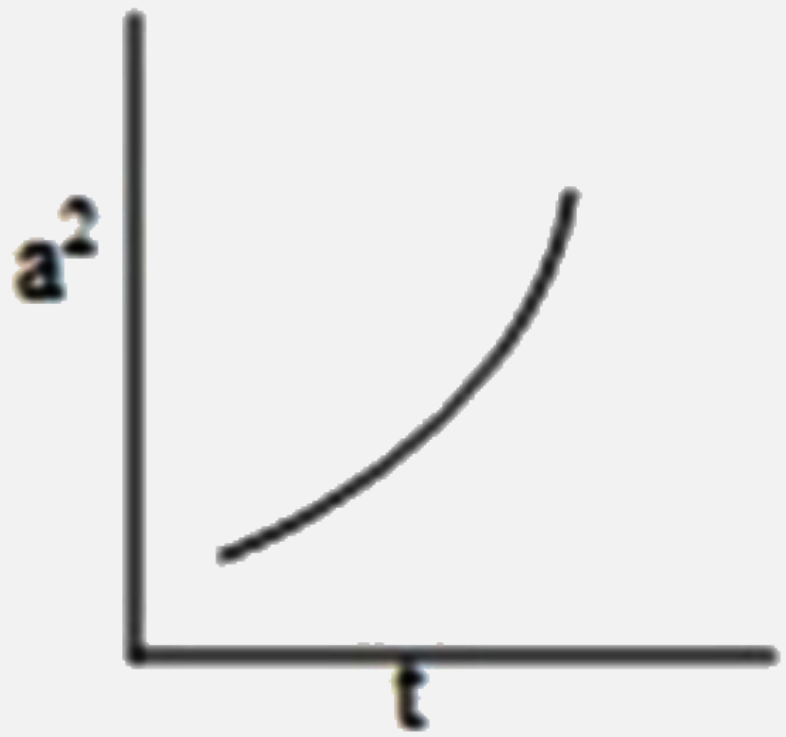 D
D
In an experiment , to find the loss of energy with respect to time in case of swinging simple pendulum , the graph between (amplitude)2 and time is
A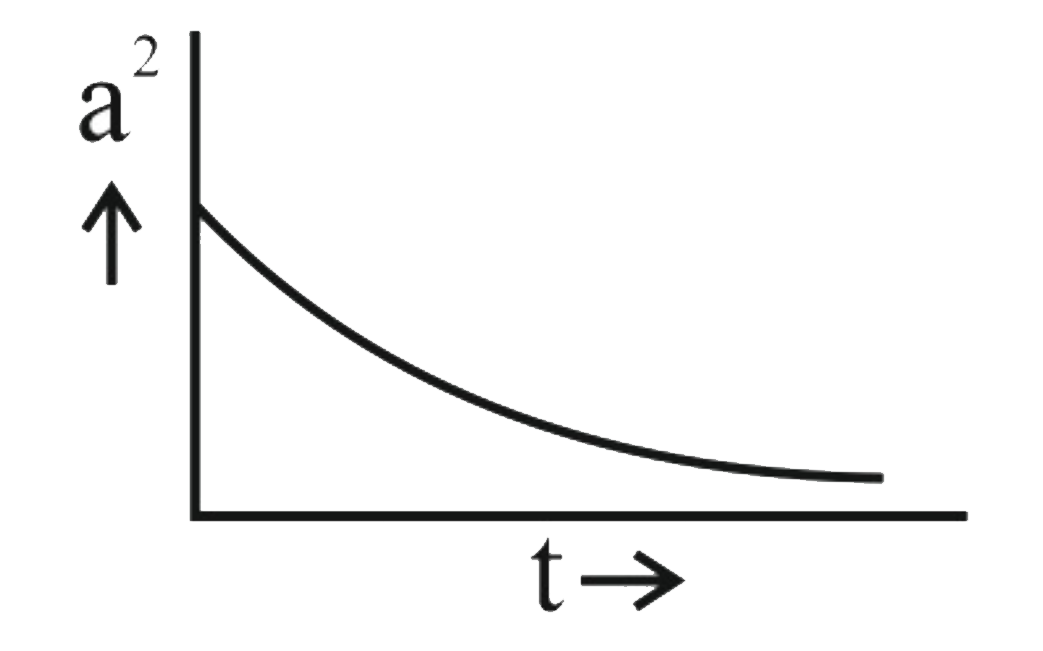 B
B C
C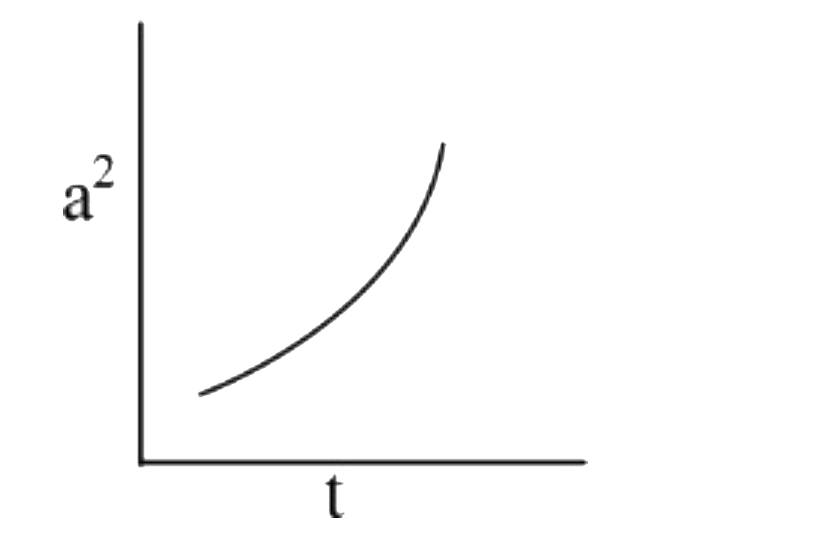 D
D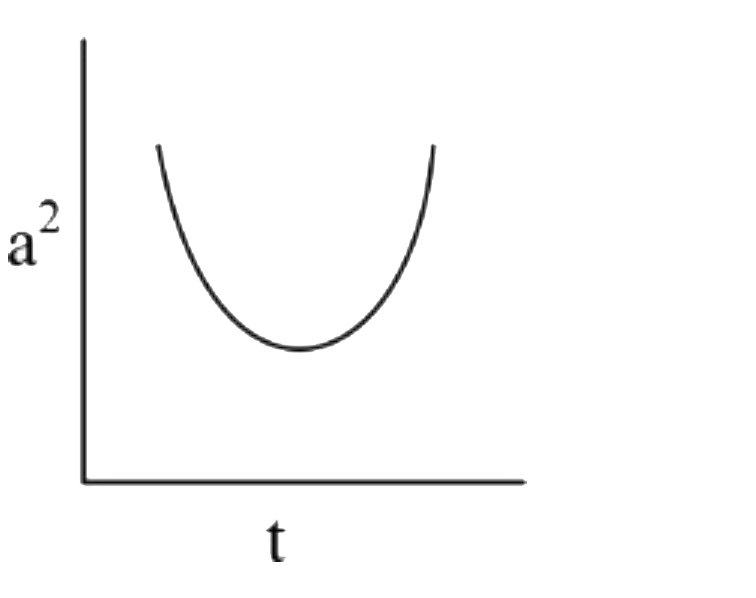
Why does a tuning fork eventually stop vibrating?
View SolutionOn what factors does the period of a simple pendulum depend ?
View SolutionWhy the oscillations of a simple pendulum are not perceived by the human ear ?
View SolutionState how does the time period of a simple pendulum depend on length of pendulum.
View SolutionA simple pendulaum consists of a small mass suspended from a string that is fixed at its upper end and has negligible mass. The length of time, t second, for complete swing of a simple pendulum can be modeled by the equation t=2π√L32, where L is the length, in feet, of the string. If the time required for a complete swing of Pendulum 1 is triple the time required for a complete swing of Pendulum 2, the length of Pendulum 1's string is how many times the length of Pendulum 2's string?
View Solution
