With what velocity should a particle be projected so that its height becomes equal to radius of earth ?
(GMR)12
(8GMR)12
(2GMR)12
(4GMR)12
Step by step video solution for With what velocity should a particle be projected so that its height becomes equal to radius of earth ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
With what minimum velocity v should a particle be thrown horizontally from a height h above the surface of the earth of mass M so that it does not fall back on the earth ? Radius of earth is R ?
View SolutionBy what facter should the velocity of a moving particle be changed so that its kinetic energy becomes 1/16 of its intial value ?
View Solution
Knowledge Check
With what velocity should a particle be projected so that is height becomes equal to radius of earth ?
A(GMR)3/2B(8GMR)1/2C(2GMR)1/2D(4GMR)1/2With what velocity should a particle be projected so that its maximum height attained becomes equal to radius of earth ?
A(GMR)1/2B(8GMR)1/2C(2GMR)1/2D(4GMR)1/2At what angle to the horizontal should an object be projected so that the maximum height reached is equal to the horizontal range.
Atanθ=2Btanθ=4Ctanθ=3Dtanθ=3
What is the value of the acceleration due to gravity at a height equal to radius of earth?
View SolutionAt what angle to the horizontal should an object be projected so that the maximum height reached is equal to the horizontal range.
View Solutionwhat should be the velocity of an electron so that its momentum becomes equal to that of a photon of wavelength 5200Å
View SolutionA body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
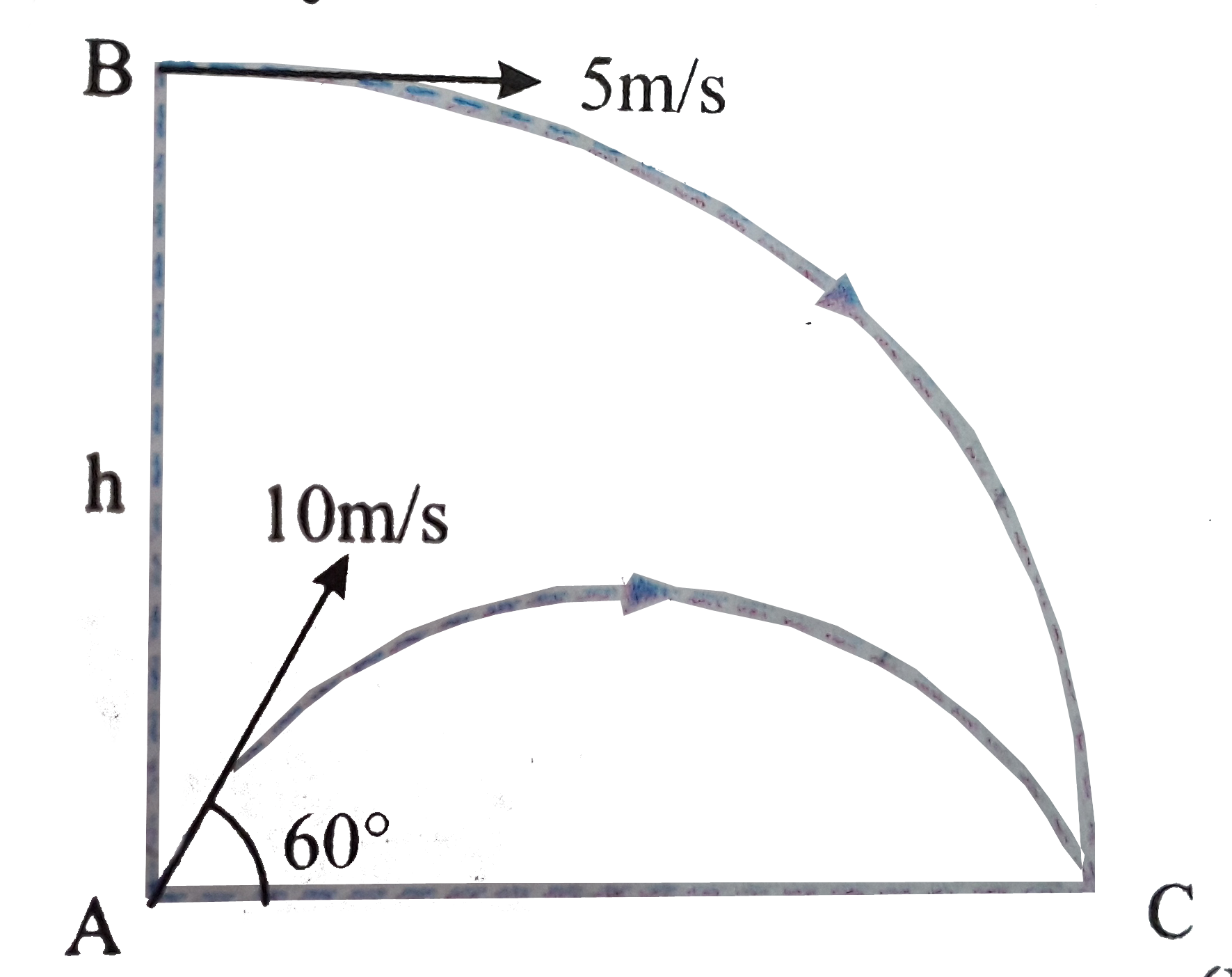
View Solution
