Would you expect the total energy of the solar system to be constant? What about the total angular momentum? Explain
To determine whether the total energy and total angular momentum of the solar system are constant, we can analyze the forces and motions involved. Here’s a step-by-step solution:
Step 1: Understanding Total Energy in the Solar System
The total energy of a system is the sum of its kinetic energy (due to motion) and potential energy (due to position). In the case of the solar system, the primary forces acting on the planets are gravitational forces.
Kinetic Energy (KE): This is the energy due to the motion of the planets as they orbit the Sun.
Potential Energy (PE): This is the gravitational potential energy between the planets and the Sun, which can be expressed as:
PE=−GMmr
where G is the gravitational constant, M is the mass of the Sun, m is the mass of the planet, and r is the distance between the planet and the Sun.
Step 2: Conservation of Energy
In a closed system where only conservative forces (like gravity) are acting, the total mechanical energy remains constant. Since gravitational forces are conservative, the total energy of the solar system can be expressed as:
Etotal=KE+PE
As the planets move in their orbits, energy can transform between kinetic and potential forms, but the total remains constant.
Step 3: Understanding Total Angular Momentum
Angular momentum (L) is a measure of the rotational motion of an object and is given by:
L=r×p
where r is the radius vector from the center of rotation (the Sun) to the object (the planet), and p is the linear momentum of the object.
Step 4: Conservation of Angular Momentum
In the solar system, the gravitational force acts as a central force directed towards the Sun. This means that the net torque (τ) about the Sun is zero:
τ=r×F=0
Since there is no net torque acting on the planets, the total angular momentum of the solar system remains constant.
Conclusion
1. Total Energy: Yes, the total energy of the solar system is constant due to the conservation of energy in a system dominated by conservative forces (gravity).
2. Total Angular Momentum: Yes, the total angular momentum of the solar system is also constant because there is no net external torque acting on the system.
The total energy of a system is the sum of its kinetic energy (due to motion) and potential energy (due to position). In the case of the solar system, the primary forces acting on the planets are gravitational forces.
PE=−GMmr
where G is the gravitational constant, M is the mass of the Sun, m is the mass of the planet, and r is the distance between the planet and the Sun.
In a closed system where only conservative forces (like gravity) are acting, the total mechanical energy remains constant. Since gravitational forces are conservative, the total energy of the solar system can be expressed as:
Etotal=KE+PE
As the planets move in their orbits, energy can transform between kinetic and potential forms, but the total remains constant.
Angular momentum (L) is a measure of the rotational motion of an object and is given by:
L=r×p
where r is the radius vector from the center of rotation (the Sun) to the object (the planet), and p is the linear momentum of the object.
In the solar system, the gravitational force acts as a central force directed towards the Sun. This means that the net torque (τ) about the Sun is zero:
τ=r×F=0
Since there is no net torque acting on the planets, the total angular momentum of the solar system remains constant.
1. Total Energy: Yes, the total energy of the solar system is constant due to the conservation of energy in a system dominated by conservative forces (gravity).
2. Total Angular Momentum: Yes, the total angular momentum of the solar system is also constant because there is no net external torque acting on the system.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.4
16 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.2
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
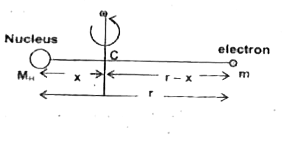
The angular momentum of the atom will be constant about an axis passing through
View SolutionThe total energy stored in the condenser system shown in the figure will be

View SolutionThe total energy stored in the condensery system shown in the figure wili be

View SolutionWhat is the minimum energy that must be given to a H atom in ground state so that it can emit an Hγ line in Balmer series. If the angular momentum of the system is conserved, what would be the angular momentum of such Hγ photon ?
View SolutionIf total energy of the same electron is E, then what would be its kinetic energy and potential energy .
View SolutionIf total energy of the same electron is E, then what would be its kinetic energy and potential energy .
View SolutionTwo particle are initially moving with angular momentum →L1 and →L2 in a region of space with no external torque. A constant external torque →τ then acts on one particle, but not on the other particle, for a time interval Δt. What is the change in the total angular momentum of the two particles ?
View SolutionIf angular momentum of a system is constant, which of the following will be zero
View SolutionThe total energy of the earth + Sun system is negative. How do you interpret the negative energy of a system?
View SolutionIn a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
View Solution
