Two particle are initially moving with angular momentum →L1 and →L2 in a region of space with no external torque. A constant external torque →τ then acts on one particle, but not on the other particle, for a time interval Δt. What is the change in the total angular momentum of the two particles ?
−−→ΔL=→L1−→L2
−−→ΔL=12(→L1−→L2)
−−→ΔL=→τΔt
−−→ΔL is not applicable for this system
The correct Answer is:C
To solve the problem, we need to analyze the situation using the principles of angular momentum and torque.
1. Understand the Initial Conditions:
- We have two particles with initial angular momentum represented as →L1 and →L2.
- The total initial angular momentum of the system (both particles) can be expressed as:
→Linitial=→L1+→L2
2. Identify the External Torque:
- A constant external torque →τ is applied to one of the particles for a time interval Δt.
- The other particle is not affected by any external torque.
3. Apply the Torque-Angular Momentum Relation:
- According to the relationship between torque and angular momentum, we have:
→τ=d→Ldt
- This implies that the change in angular momentum Δ→L due to the applied torque over the time interval Δt can be expressed as:
Δ→L=→τ⋅Δt
4. Calculate the Change in Total Angular Momentum:
- Since the torque is only acting on one particle, the total change in angular momentum of the system (both particles) will be equal to the change in angular momentum of the particle experiencing the torque:
Δ→Ltotal=Δ→L=→τ⋅Δt
5. Final Result:
- Therefore, the change in the total angular momentum of the two particles is:
Δ→Ltotal=→τΔt
Conclusion:
The change in the total angular momentum of the two particles when a constant external torque acts on one of them for a time interval Δt is given by →τΔt.
- We have two particles with initial angular momentum represented as →L1 and →L2.
- The total initial angular momentum of the system (both particles) can be expressed as:
→Linitial=→L1+→L2
- A constant external torque →τ is applied to one of the particles for a time interval Δt.
- The other particle is not affected by any external torque.
- According to the relationship between torque and angular momentum, we have:
→τ=d→Ldt
- This implies that the change in angular momentum Δ→L due to the applied torque over the time interval Δt can be expressed as:
Δ→L=→τ⋅Δt
- Since the torque is only acting on one particle, the total change in angular momentum of the system (both particles) will be equal to the change in angular momentum of the particle experiencing the torque:
Δ→Ltotal=Δ→L=→τ⋅Δt
- Therefore, the change in the total angular momentum of the two particles is:
Δ→Ltotal=→τΔt
The change in the total angular momentum of the two particles when a constant external torque acts on one of them for a time interval Δt is given by →τΔt.
Similar Questions
Two particle A and B are moving as shown in the figure
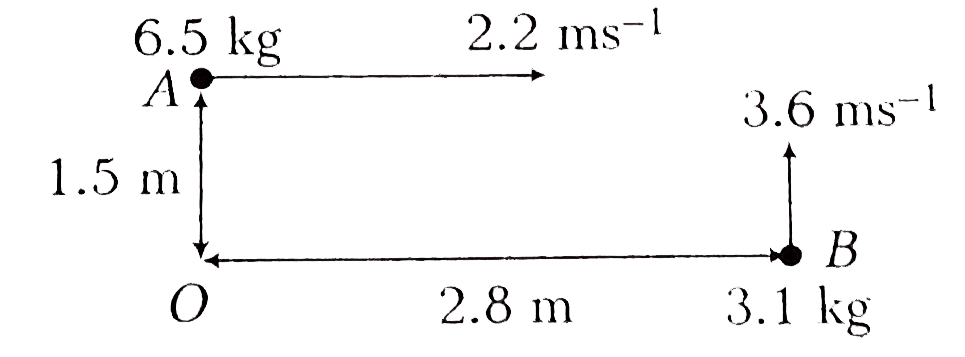
Their total angular momentum about the point O is
View SolutionA torque of 5Nm is applied on a particle for 2 seconds, calculate the change in its angular momentum.
View SolutionA torque of 5Nm is applied on a particle for 2 seconds, calculate the change in its angular momentum.
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionFor of particles under central forcer field, the total angular momentum is conserved.
The torque acting on such a system is zero.
View SolutionWhat is the magnitude of torque acting on a particle moving in the xy - plane about the origin if its angular momentum is 4.0√tkgm2s−1 ?
View SolutionThe linear momentum of a particle as a fuction of time 't' is given by , p = a +bt , where a and b are positive constants . What is the force acting on the particle ?
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionThe torque acting on a particle about an arbitrary origin is zero, what can you say about its angular momentum' ?
View SolutionA particle of mass is moving in a straight line with momentum p. Starting at time t= 0, a force F= kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is constant . The value of T is :
View Solution
