x and y displacements of a particle are given as x(t)=−asinωt and y(t)=asin2ωt. Its trajectory will look like.
A
B

C
D

Video Solution
Text Solution
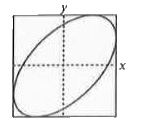
The correct Answer is:C
Here, x=asinωt
y=asin2ωt
y=2asinωtcosωt
y=2x√1−x2a2
y=2ax√(a−x)(a+x)
y=0, at x=0,±a
|
Topper's Solved these Questions
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - NEET CAFÉ TOPICWISE PRACTICE QUESTIONS
200 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - CHECK YOUR NEET VITALS
25 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
Similar Questions
Knowledge Check
The displacement of a particle is given by x=cos2ωt. The motion is
Asimple harmonicBperiodic but not simple harmonicCperiodic but not simple harmonicDNone of the aboveThe displacemeent of a particle is given at time t by x=Asin(−2ωt)+Bsin2ωt. Then,
Athe motion of the particle is SHM with an amplitude of √A2+B24Bthe motion of the particle is not SHM, but oscillatory with a time period of T=πω.Cthe motion of the particle is oscillatory with a time period of T=π2ω.Dthe motion of the particle is a not periodicThe displacement of a particle is given at time t, by:
x=Asin(−2ωt)+Bsin2ωt Then,Athe motion of the particle is SHM with an amplitude of √A2+B24Bthe motion of the particle is not SHM, but oscillatory with a time period of T=π/ωCthe motion of the particle is oscillatory with a time period of T=π/2ωDnone
A particle is acted simultaneously by mutually perpendicular simple hormonic motions x=acosωtandy=asinωt. The trajectory of motion of the particle will be
View SolutionA particle is acted simultaneously by mutually perpendicular simple harmonic motions x=a cosωt and y=asinωt. The trajectory of motion of the particle will be
View SolutionA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is

View SolutionA particle is acted simultaneously by mutally perpendicular simple harmonic motion x=acosωt and y=asinωt. The trajectory of motion of the particle will be
View SolutionA particle moves in x-y plane according to rule x=asinωt and y=−acosωt. The particle follows
View Solution
