X-ray are produced in an X-ray tube operating at a given accelerating voltage. The wavelength of the continuous X-ray has values from. (a) 0→∞
(b) λmin→∞,whereλmin>0
(c ) 0 to λmax,whereλmax<∞
(d) λminotλmax, where 0<λ(min)<λmax<∞
The correct Answer is:B
To solve the problem regarding the wavelength of continuous X-rays produced in an X-ray tube operating at a given accelerating voltage, we can analyze the situation step by step.
1. Understanding X-ray Production:
- X-rays are produced when high-energy electrons collide with a metal target in an X-ray tube. The energy of the electrons is determined by the accelerating voltage applied to them.
2. Energy and Wavelength Relationship:
- The energy of the emitted X-ray photons is related to their wavelength by the equation:
E=hcλ
where E is the energy of the photon, h is Planck's constant, c is the speed of light, and λ is the wavelength.
3. Determining Minimum Wavelength:
- The maximum energy of the X-ray photon corresponds to the maximum kinetic energy of the electrons, which is equal to the accelerating voltage (in electron volts). Therefore, the minimum wavelength (λmin) can be calculated using:
λmin=hcEmax
- Since Emax=eV (where e is the charge of the electron and V is the accelerating voltage), we find that λmin is greater than 0.
4. Determining Maximum Wavelength:
- The maximum wavelength (λmax) is not defined by the energy of the electrons but rather represents the continuous spectrum of X-rays produced. Theoretically, it can extend to infinity, but practically, it is limited by the energy of the electrons.
5. Conclusion:
- Therefore, the wavelength of continuous X-rays produced in an X-ray tube ranges from λmin (which is greater than 0) to λmax (which can be considered as infinity). This leads us to the conclusion that the correct answer is:
(b) λmin to ∞, where λmin>0
- X-rays are produced when high-energy electrons collide with a metal target in an X-ray tube. The energy of the electrons is determined by the accelerating voltage applied to them.
- The energy of the emitted X-ray photons is related to their wavelength by the equation:
E=hcλ
where E is the energy of the photon, h is Planck's constant, c is the speed of light, and λ is the wavelength.
- The maximum energy of the X-ray photon corresponds to the maximum kinetic energy of the electrons, which is equal to the accelerating voltage (in electron volts). Therefore, the minimum wavelength (λmin) can be calculated using:
λmin=hcEmax
- Since Emax=eV (where e is the charge of the electron and V is the accelerating voltage), we find that λmin is greater than 0.
- The maximum wavelength (λmax) is not defined by the energy of the electrons but rather represents the continuous spectrum of X-rays produced. Theoretically, it can extend to infinity, but practically, it is limited by the energy of the electrons.
- Therefore, the wavelength of continuous X-rays produced in an X-ray tube ranges from λmin (which is greater than 0) to λmax (which can be considered as infinity). This leads us to the conclusion that the correct answer is:
(b) λmin to ∞, where λmin>0
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.4
8 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level -1 Assertion And Reason
10 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.2
12 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
Knowledge Check
If the equation x23−λ+y2λ−8+1=0 represents an ellipse, then
(i) λ<8
(ii) λ>3
(iii) 3<λ<8
(iv) λ<3 or λ>8Aλ<8Bλ>3C3<λ<8Dλ<3 or λ>8Electrons with de-Broglie wavelength λ fall on the target in an X-ray tube. The cut-off wavelength of the emitted X-ray is
Aλ0=2mcλ2hBλ0=2hmcCλ0=2m2c2λ2h2Dλ0=λ
Electrons with de - Brogli wavelengtyh λ fall on the target in
an X-ray tube.The cut off wavelength of the emitted Xrays is
(a) λ0=2mcλ2h (b)λ0=2hmc
(c ) λ02m2c2λ3h2 (d)λ0=λ
View SolutionThe equation of the locus of the foot of perpendicular drawn from (5, 6) on the family of lines (x−2)+λ(y−3)=0 (where λ∈R) is
View SolutionAn X-ray tube operated at 40kV emits a continous X-ray spectrum with a short wavelength limit λmin=0.310Å. Calculate Plank's constant.
View SolutionFor lyman series λmax -λmin = 340Angstrom . Find same for paschen series
View SolutionElectrons with de-Broglie wavelength λ fall on the target in an X-ray tube. The cut-off wavelength of the emitted X-ray is
View SolutionThe intensity of X-rays form a Coolidge tube is plotted against wavelength λ as shown in the figure. The minimum wavelength found is λc and the wavelength of the Kα line is λk. As the accelerating voltage is increased
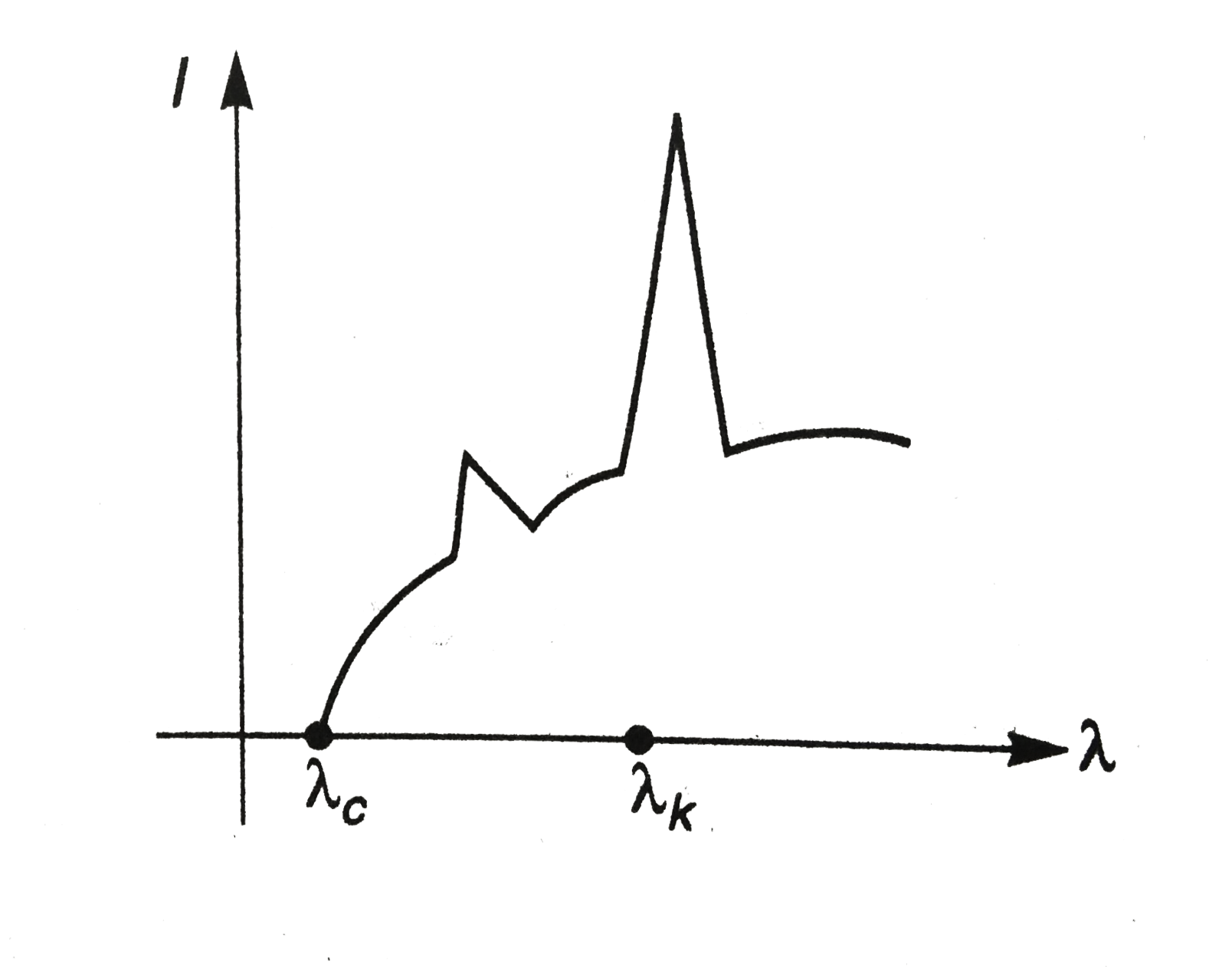
(a) λk−λc increases (b) λk−λc decreases
(c ) λk increases (d) λk decreases
View Solution
