The minimum wavelength λmin in the continuous spectrum of X-rays is
Proportional to the potential difference V between the cathode and anode.
Inversely proportional to potential differece V between the cathode and anode
Proportional to the square root of the potential difference V between the cathode and the anode.
Inversely proportional to the square root of the potential difference V between the cathode and the anode.
The correct Answer is:B
To find the minimum wavelength λmin in the continuous spectrum of X-rays, we can use the relationship between the minimum wavelength and the kinetic energy of the electrons that produce the X-rays.
1. Understanding the Kinetic Energy:
The kinetic energy (KE) of the electrons when they are accelerated through a potential difference V is given by:
KE=eV
where e is the charge of the electron.
2. Relating Kinetic Energy to Wavelength:
The energy of a photon can also be expressed in terms of its wavelength λ using the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
3. Setting the Energies Equal:
For the minimum wavelength of X-rays, the kinetic energy of the electrons is converted into the energy of the X-ray photon. Therefore, we can set the two expressions for energy equal:
eV=hcλmin
4. Rearranging for Wavelength:
Rearranging the equation to solve for λmin:
λmin=hceV
5. Analyzing the Relationship:
From the equation λmin=hceV, we can see that λmin is inversely proportional to the potential difference V. This means that as the potential difference increases, the minimum wavelength decreases.
6. Conclusion:
Therefore, the minimum wavelength in the continuous spectrum of X-rays is inversely proportional to the potential difference V.
Final Answer:
The minimum wavelength λmin in the continuous spectrum of X-rays is inversely proportional to the potential difference V.
The kinetic energy (KE) of the electrons when they are accelerated through a potential difference V is given by:
KE=eV
where e is the charge of the electron.
The energy of a photon can also be expressed in terms of its wavelength λ using the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
For the minimum wavelength of X-rays, the kinetic energy of the electrons is converted into the energy of the X-ray photon. Therefore, we can set the two expressions for energy equal:
eV=hcλmin
Rearranging the equation to solve for λmin:
λmin=hceV
From the equation λmin=hceV, we can see that λmin is inversely proportional to the potential difference V. This means that as the potential difference increases, the minimum wavelength decreases.
Therefore, the minimum wavelength in the continuous spectrum of X-rays is inversely proportional to the potential difference V.
The minimum wavelength λmin in the continuous spectrum of X-rays is inversely proportional to the potential difference V.
Topper's Solved these Questions
Similar Questions
A X-ray tube operates at an accelerating potntial of 20 kV. Which of the following wavelength will be absent in the continuous spectrum of X-rays ?
View SolutionIn a Coolidege tube experiment, the minimum wavelength of the continuouse X-ray spectrum is equal to 66.3 om . Then
View SolutionContinuous spectrum is produced by
View SolutionA beam of electrons having energy 28 keV each strikes a target generating X rays. The minimum wave length λmin (called cut off wavelength ) of the X rays generated is
View SolutionThe intensity of X- ray from a coolidge tube is plotted againest wavelength λ as shown in the figure . The minimum wavelength found λc and the wavelength of theka line is λk, As the accelerating voliage is increase
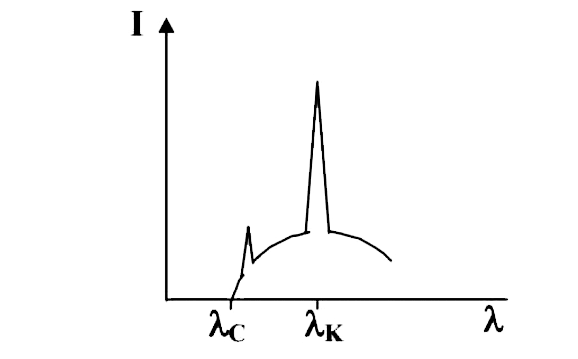
View Solutionin order that the short wavelength limit of the continuous X-ray spectrum be 1Å, the potential difference through which an electron must be accelerated is
View SolutionIf there times of λmin of continuous X−ray spectrum of target metal at 40kV is some as the wavelength of Kα line of this metal at 30kV, then determine the atomic number of the target metal.
View SolutionConsider the following two statements A and B and identify the correct choice in the given answer
A : The characteristic X-ray spectrum depends on the nature of the material of the target
B : The short wavelength limit of continuous X-ray spectrum varies inversely with the potential difference applied to the X-rays tube
View SolutionThe wavelength interval between kα line and λmin of continuous X-ray spectrum of metal becomes 2 times when operating voltage is charged from 10 kV to x kV. Find x. What will happen to wavelength interval between kα line and kβ line in this case ? (Z=28)
View SolutionFind the cutoff wavelength for the continuous X-rays coming form an X-ray tube operating at 30 kV.
View Solution