x−y is the vertical plane as shown in figure. A particle of mass 1kg is at (10m,20m) at time t=0. It is released from rest. Another particles of mass 2kg is at (20m,40m) at the same instant. It is projected with velocity (10ˆi+10ˆj)m/s. After 1s. Find (a) acceleration (b)velocity (c) position of the center of mass
The correct Answer is:A, B, C
(a) aCOM=m1a1+m2a2m1+m2
=(1)(−10ˆj)+(2)(−10ˆj)1+2
=(−10ˆj)m/s2
(b) vCOM=m1v1+m2v2m1+m2
=m1(u1+a1t)+m2(u2+a2t)m1+m2
=(1)[0+(−10ˆj)(1)]+2[(10ˆi+10ˆj)+(−10ˆj)(1)]1+2
=103(2ˆi−ˆj)m/s
(c) rCM=m1r1+m2r2m1+m2
=m1[r1+ut+12at2]1+m2[r1+ut+12at2]2m1+m2
=1[(10ˆi+20ˆj)+0+12(−10ˆj)(1)2]+2[(20ˆi+40ˆj)+(10ˆi+10ˆj)(1)+12(−10ˆj)(1)2]1+2
=(703ˆi+35ˆj)m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A particle is projected from ground with velocity 40(√2)m/s at 45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View SolutionA particle of mass 2kg located at the position (ˆi+ˆj)m has velocity 2(ˆi−ˆj+ˆk)m/s . Its angular momentum about Z-axis in kgm2/s is
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionA block of mass 1kg is at x=10m and moving towards negative x−aξs with velocity 6m/s. Another block of mass 2kg is at x=12m and moving towards positive x−axis with velocity 4m/s at the same instant. Find position of their centre of mass after 2s.
View SolutionDisplacement of a particle of mass 2 kg varies with time as s=(2t2−2t+10)m. Find total work done on the particle in a time interval from t=0 to t=2s.
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionA particle of mass 1 kg is projected upwards with velocity 60 m/s. Another particle of mass 2 kg is just deopper from a certain height. After 2 kg is just of the particles have colliided with ground, match the following [ Take g= 10 m/s2]
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
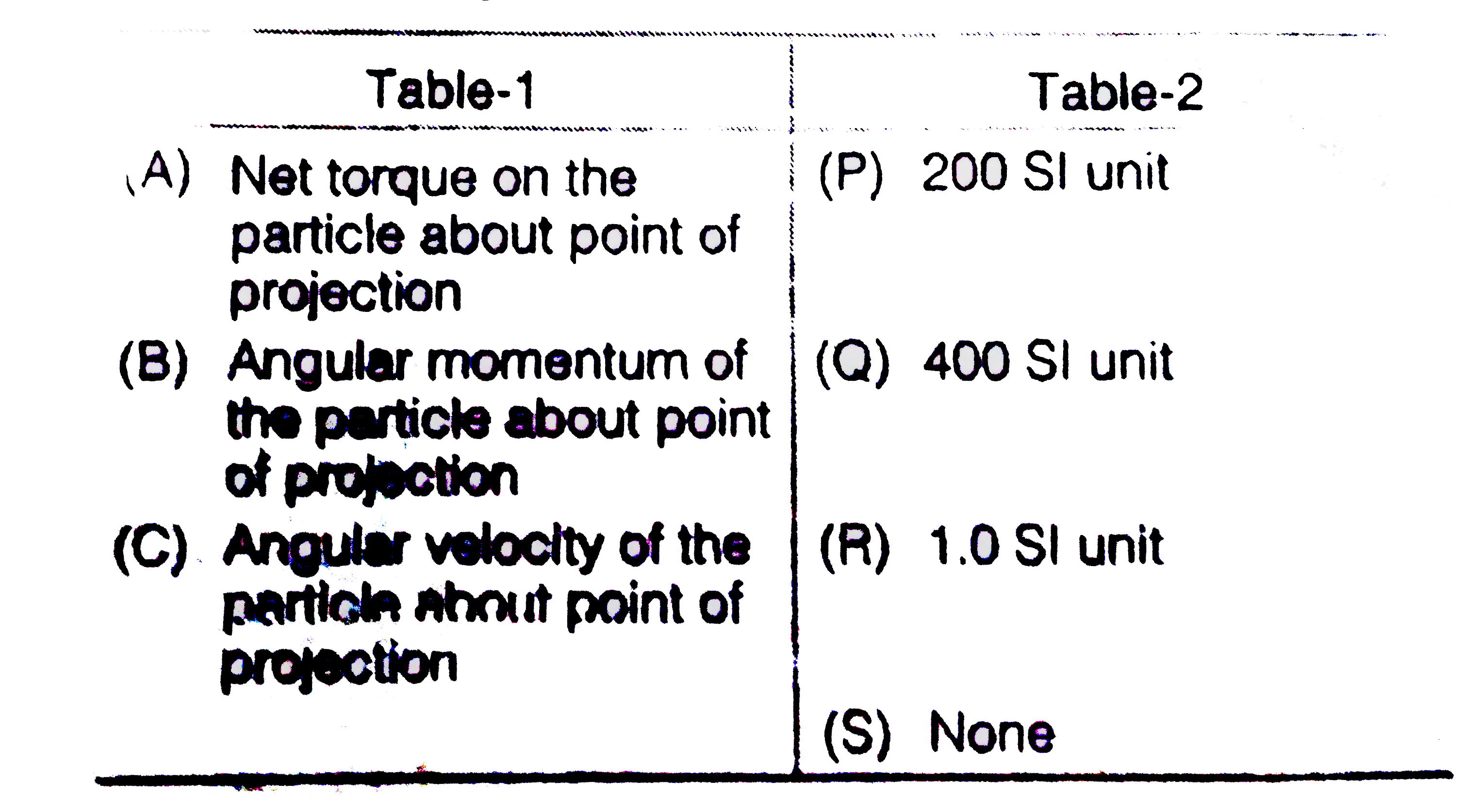
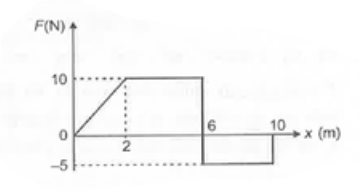
View SolutionThe force versus position (F-x) graph of a particle of mass 2 kg is shown in the figure. If at x = 0 velocity of particle is 2 m/s then velocity of the particle at x = 8 m will be
View SolutionA particle starts from the origin at t = 0 s with a velocity of 10.0ˆj m/s and moves in plane with a constant acceleration of (8ˆi+2ˆj)ms−2. The y-coordinate of the particle in 2 sec is
View Solution
