Young's modulus of brass and steel are 10×1010N/m2 and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS respectively. Then
RS=√2RB
RS=RB√2
RS=4RB
RS=RB4
The correct Answer is:B
Y=FπR2×l△l
F, l and △l are constant.
R2∝1Y
R2SR2B=YBYS=10112×1011=12
or RSRB=1√2 or RS=RS√2
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning20videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - NEET Questions17videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Viscosity29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Young's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
ARs=√2RBBRS=RB√2CRS=4RBDRS=(RB)/4 - Question 2 - Select One
The Young's modulus of brass and steel are 10×1010Nm−2and20×1010Nm−2 respectively. A brass wire and steel wire of the same length are extended by 1 mm under the same force. If the radii of the brass and steel wires are RBandRS respectively, then
ARS=RB4BRS=4RBCRS=√2,RBDRS=RB√2 - Question 3 - Select One
The young 's modulus of brass and steel are 1.0×1011Nm−2 and 2.0×1011N/m2. Respectively . A brass wire and steel wire of the same length extend by 1 mm, each under the same forece . It radii of brass and steel wires are RB and RS respectively, them
ARs=√2RBBRs=RB√2CRs=4RBDRS=RB2
A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
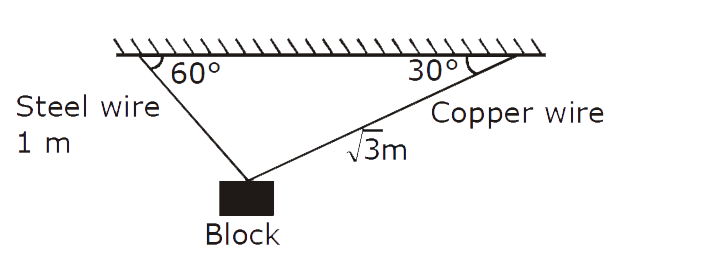
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011Nm−2 and 2.0×1011Nm−2. A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of brass and steel wires are RB and Rs respectively, then
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
View SolutionYoung's modulus for steel is 2×1010N/m2. If the interatomic distance for steel is 3 Å, then the interatomic force constant for steel will be
View Solution

