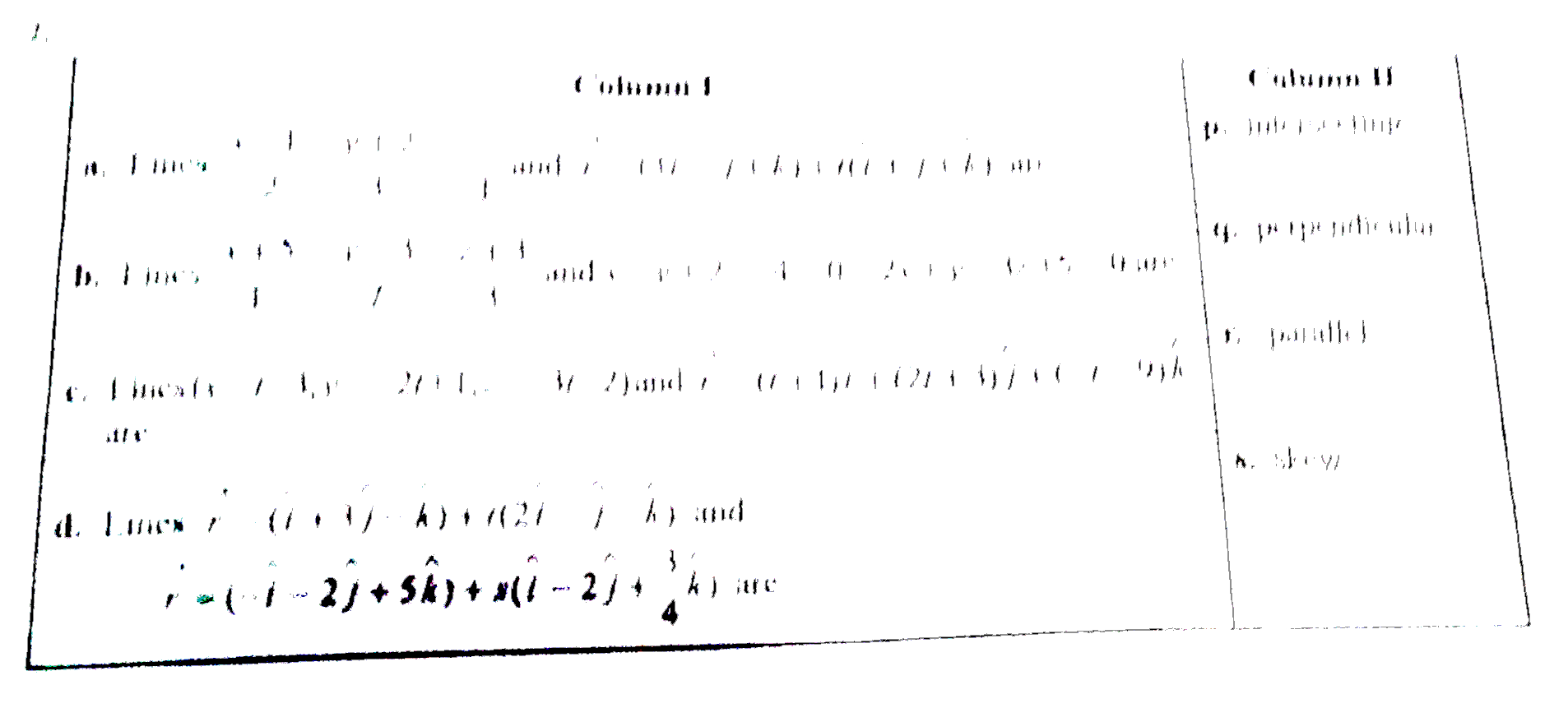The correct Answer is:a→q,s;b→r;c→p,q;d→p
a. Line x−1−2=y+23=z−1 is along the vector →a=−2ˆi+3ˆj−ˆk and line →r=(3ˆi−ˆj+ˆk)+t(ˆi+ˆj+ˆk) is along the vector →b=ˆi+ˆj+ˆk. Here →a⊥→b.
Also ∣∣
∣
∣∣3−1−1−(−2)1−0−23−1111∣∣
∣
∣∣≠0
b. The direction ratios of the line x−y+2z−4=0
=2x+y−3z+5=0 are ∣∣
∣
∣∣ˆiˆjˆk1−1221−3∣∣
∣
∣∣=ˆi+7ˆj+3ˆk.
Hence, the given two lines are parallel.
c. The given lines are (x=t−3,y=−2t+1,z=−3t−2)and→r=(t+1)ˆi+(2t+3)ˆj+(−t−9)ˆk, or
x+31=y−1−2=z+2−3andx−11=y−32=z+9−1.
The lines are perpendicular as
(1)(1)+(−2)(2)+(−3)(−1)=0.
Also ∣∣
∣
∣∣−3−11−3−2−(−9)1−2−312−1∣∣
∣
∣∣=0
Hence, the lines are intersecting.
d. The given lines are →r=(ˆi+3ˆj−ˆk)+t(2ˆi−ˆj−ˆk)and→r=(−ˆi−2ˆj+5ˆk)+s(ˆi−2ˆj+34ˆk).
∣∣
∣
∣∣1−(−1)3−(−2)−1−52−1−11−23/4∣∣
∣
∣∣=0
Hence, the lines are coplanar and intersecting (as the lines are not parallel).
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Numerical)
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - JEE Previous Year
26 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Comprehension)
12 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
- TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank
34 Videos
Similar Questions
Find the number of sphere of radius r touching the coordinate axes.
View Solution(i) Find the equation of the plane passing through the points(2,1,0),(5,0,1)and(4,11). (ii) If P s the point (2,1,6), then the find the point Q such that PQ is perpendicular to the plane in (i) and the midpoint of PQ lies on it.
View SolutionGiven four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is
View SolutionLet the line L1:x−12=y−23=z−34 and L2:x−21=y−32=z−k4 intersect at P.The least distance of P from the plane 3x−4y−12z+4=0, equals
View SolutionNumber of solutions of the equation
sin7θ=sinθ+sin3θ∈0<θ<π2 is equal to
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution