The correct Answer is:a→p;b→q,s;c→p;d→p,q
sinA,sinB are roots of c2x2−c(a+b)x+ab=0
∴sinA+sinB=c(a+b)c2
⇒(a+b)2R=c(a+b)c2 or 2R=c ...(i)
From sine formula, we have
asinA=bsinB=csinC=2R=c [using Eq. (i)] ltbr or sinC=1 or C=90∘
b. Using cosine formula, we have
cos30∘=402+(40√3)2−a22×40×40√3
or a=40

Thus, AB=BC=40, i.e., ΔABC is isoceles.
Also, ∠A=∠C=30∘
⇒∠B=120∘
Therefore, ΔABC is an obtuse -angled triangle
c. 81sin2x+81cos2x=30
or 81sin2x+8181sin2x=30
Put 81sin2x=t
t+81t=30
or t=27,t=3
When t=3,81sin2x=3
or 34sin2x=3
or x=30∘
When t=27,34sin2x=33
⇒x=60∘
Therefore, the triangle is right angled
d. In ΔABC,
cosAcosB+sinAsinBsinC=1
⇒sinC=1−cosAcosBsinAsinB...(i)
[ ∵∠C is an angle of the triangle]
Since 0<sinC≤1, we have
0<1−cosAcosBsinAsinB≤1
or 1−cosAcosB≤sinAsinB
or 1≤sinAsinB+cosAcosB
or 1≤cos(A−B)orcos(A−B)≥1
or cos(A−B)=1
or A−B=0 or A=B ....(ii)
Also from Eq. (i) and (ii),
sinC=1−cos2Asin2A
sinC=1 or C=90∘....(iii)
From Eqs. (ii) and (iii), ΔABC is a right -angled isosceles triangle
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Numerical)
22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Main Previous Year
2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Comprehension)
34 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
Suppose α,β,γandδ are the interior angles of regular pentagon, hexagon, decagon, and dodecagon, respectively, then the value of |cosαsecβcosγcosecδ| is _________
View SolutionFor a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is There is a regular polygon with rR=1√2 (17) There is a regular polygon with rR=23 (30) There is a regular polygon with rR=√32 (47) There is a regular polygon with rR=12 (60)
View SolutionGiven that Δ=6,r1=3,r3=6
Circumradius R is equal to
View SolutionMatch the statements /expression given in List I with the values given in List II.

View SolutionThe area of a right triangle is 6864 square units. If the ratio of its legs is 143:24, then find the radius of the circle inscribed in the triangle.
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
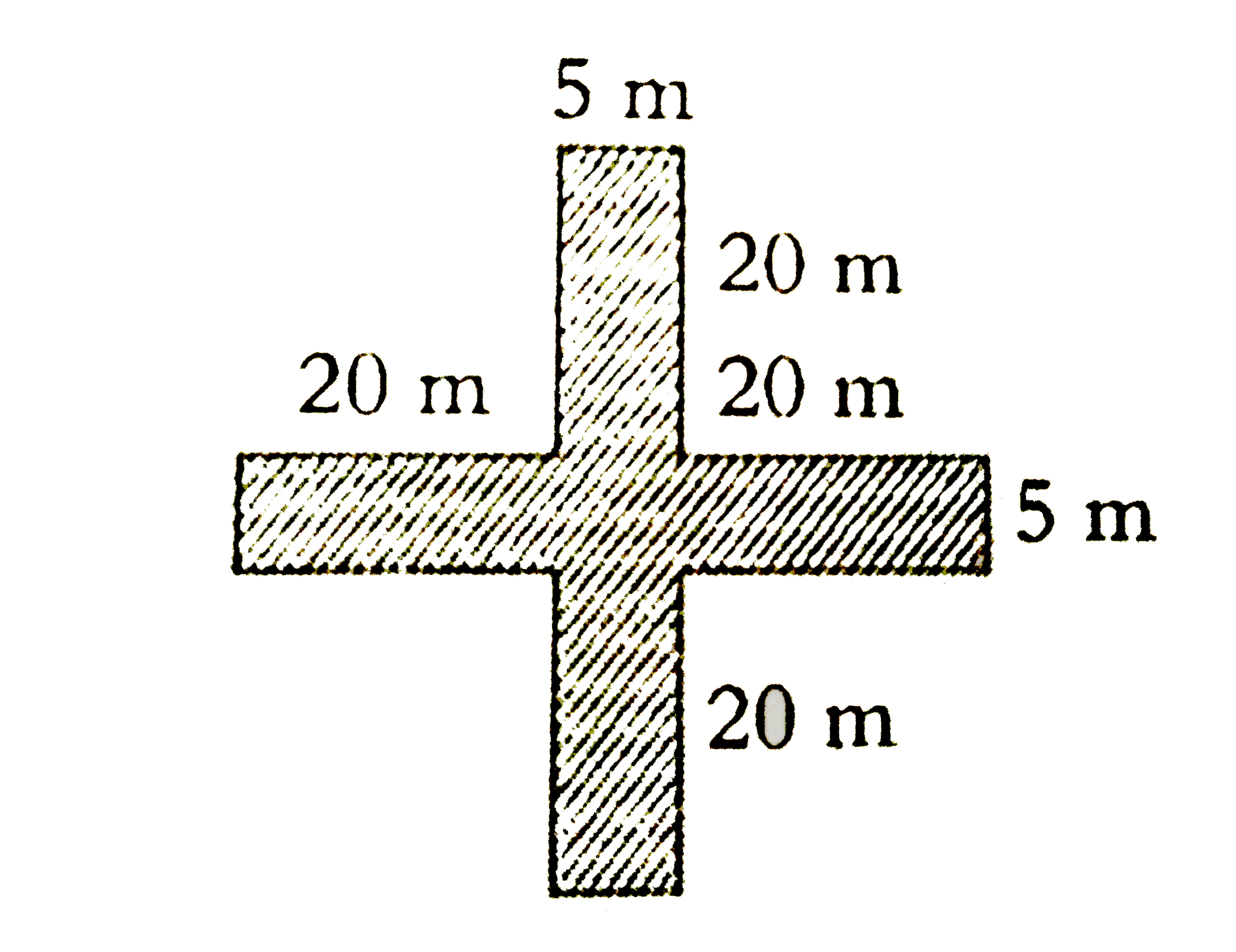
View SolutionThe area of the shaded part in the figure given below is ______.
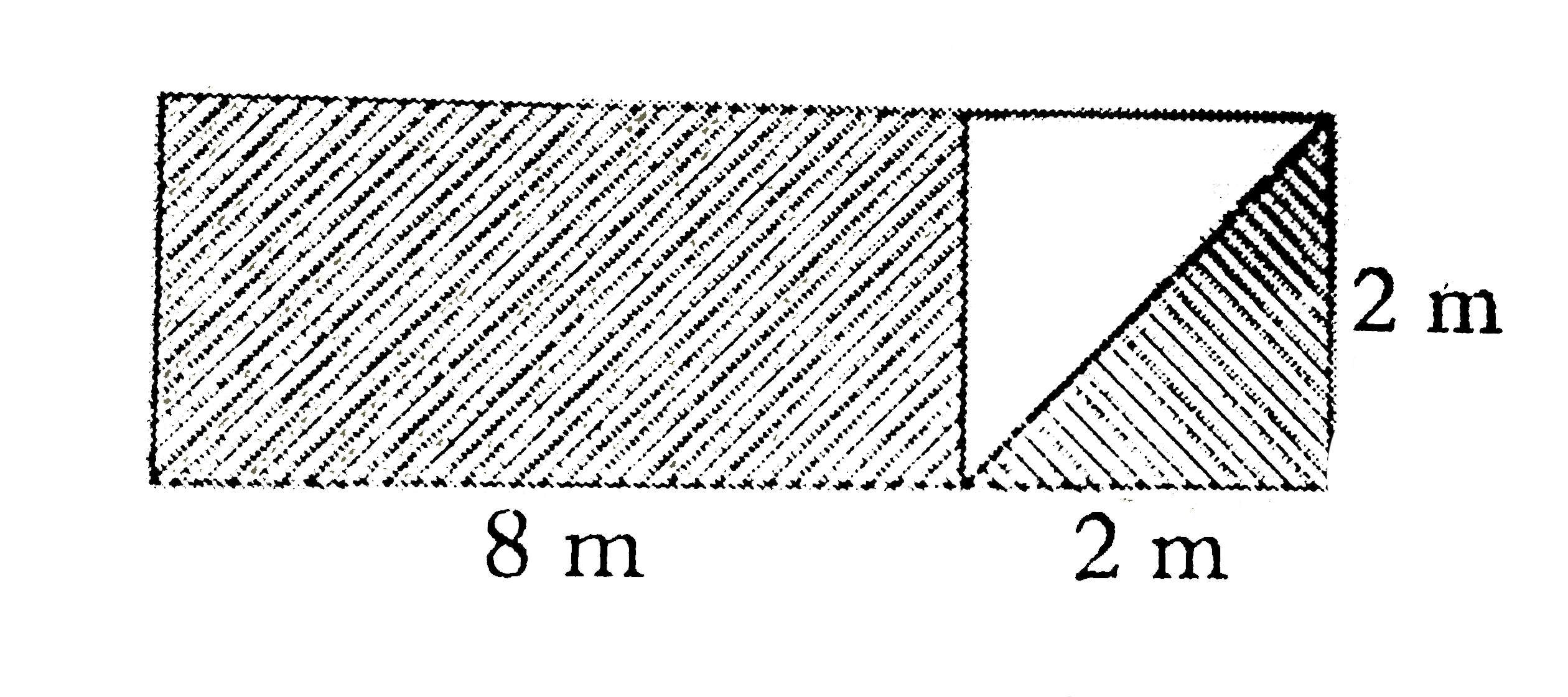
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

