In triangle ABC, AD is prependicular to BC and DE is perpendicular to AB

abcdprqq
abcdqrps
abcdspqr
abcdrpsq
The correct Answer is:D

a. Area of ΔADB=12AD×BD
=12csinB×ccosB
=c24sin2B
b. Area of ΔADC=12AD×CD
=12bsinC×bcosC=b24sin2C
c. Area of ΔADE=12AE×DE
=12ADcos(π2−B)ADsin(π2−B)
=14AD2sin2B
=14c2sin2Bsin2B
d. Area of ΔBDE=12BE×DE
=12BDcosB×ADsin(π2−B)
=12ccosBcosB×csinBcosB
=14c2cos2Bsin2B
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Numerical)
22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Main Previous Year
2 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Comprehension)
34 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
In Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
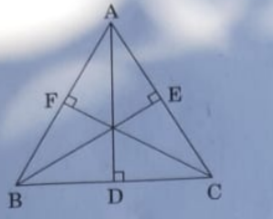
View SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4 (AD^2 +BE^2 +CF^2)=9AB^2
View Solution
Knowledge Check
In an isosceles triangle ABC with AB=AC and AD is perpendicular to BC, if AD=6 cm and the perimeter of ΔABC is 36 cm,, then the area of ΔABC is :
A54cm2B64cm2C45cm2D48cm2In triangle ABC,∠BAC=90∘and AD is perpendicular to BC. If AD=6cmand BD=4cm, then the length of BC is:
A10 cmB12 cmC13 cmD15 cm.
In a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
View SolutionIn a triangle ABC, ∠BAC=90∘, AD is the altitude from A on to BC. Draw DE perpendicular to AC and DF perpendicular to AB. Suppose AB =15 and BC = 25. Then the length of EF is
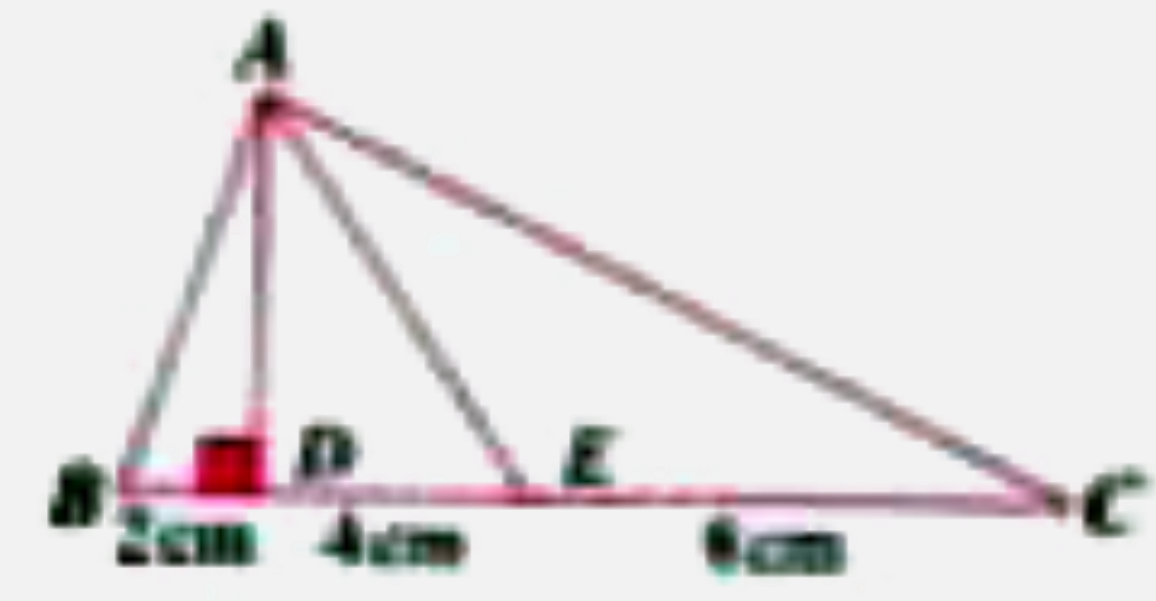
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
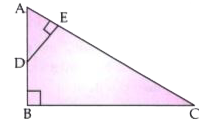
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionIn a triangle ABC, AD is perpendicular on BC. If ∠BAC=90∘,AB=c,BC=a,CA=b and AD = p, then which one of the following is correct?
View Solution
