The correct Answer is:a→q;b→s;c→p;d→r.
a. 5sinθ+3(sinθcosα−cosθsinα)
=(5+3cosα)sinθ−3sinαcosθ
⇒maxθ∈R{5sinθ+3sin(θ−α)}
=√(5+3cosα)2+9sin2α
=√34+30cosα
Therefore, the given equation is
34+30cosα=49
or cosα=1/2
⇒α=2nπ±π/3,n∈Z
b. (cosx)sin2x−3sinx+2=1
⇒sin2x−3sinx+2=0
⇒(sinx−2)(sinx−1)=0
⇒sinx=1
But this does not satisfy the equation because 0∘=1 is absurd.
c. √(sinx)+21/4cosx=0 ...(i)
∴√(sinx)>0 and so cosx<0,
Also sinx>0⇒x lies in the second quadrant
Equation (i) can be rewritten as
21/4cosx=−√(sinx)
On squaring, we get √2cos2x=sinx
or √2sin∘x+sinx−√2=0
or (√2sinx−1)(sinx+√2)=0
sinx≠−√2, therefore sinx=1/√2 ...(ii)
⇒x=3π/4 and so the general value of x is given by
x=2nπ+3π/4,n∈Z
d. log5tanx=(log54)(log4(3sinx))
⇒log5tanx=log5(3sinx) ...(i)
Since logx is real when x>0, we have
tanx>0,sinx>0
Therefore, x lies in the first quadrant. Now Eq. (i) gives
tanx=3sinxorcosx=1/3
∴x=2nπ+cos−1(1/3),n∈Z
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
Match the statements/expressions in List I with statements/expressions in List II.

View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionIf the distance between the plane ax 2y + z = d and the plane containing the lines x−12=y−23=z−34 and x−23=y−34=z−45 is √6 , then value of |d| is
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
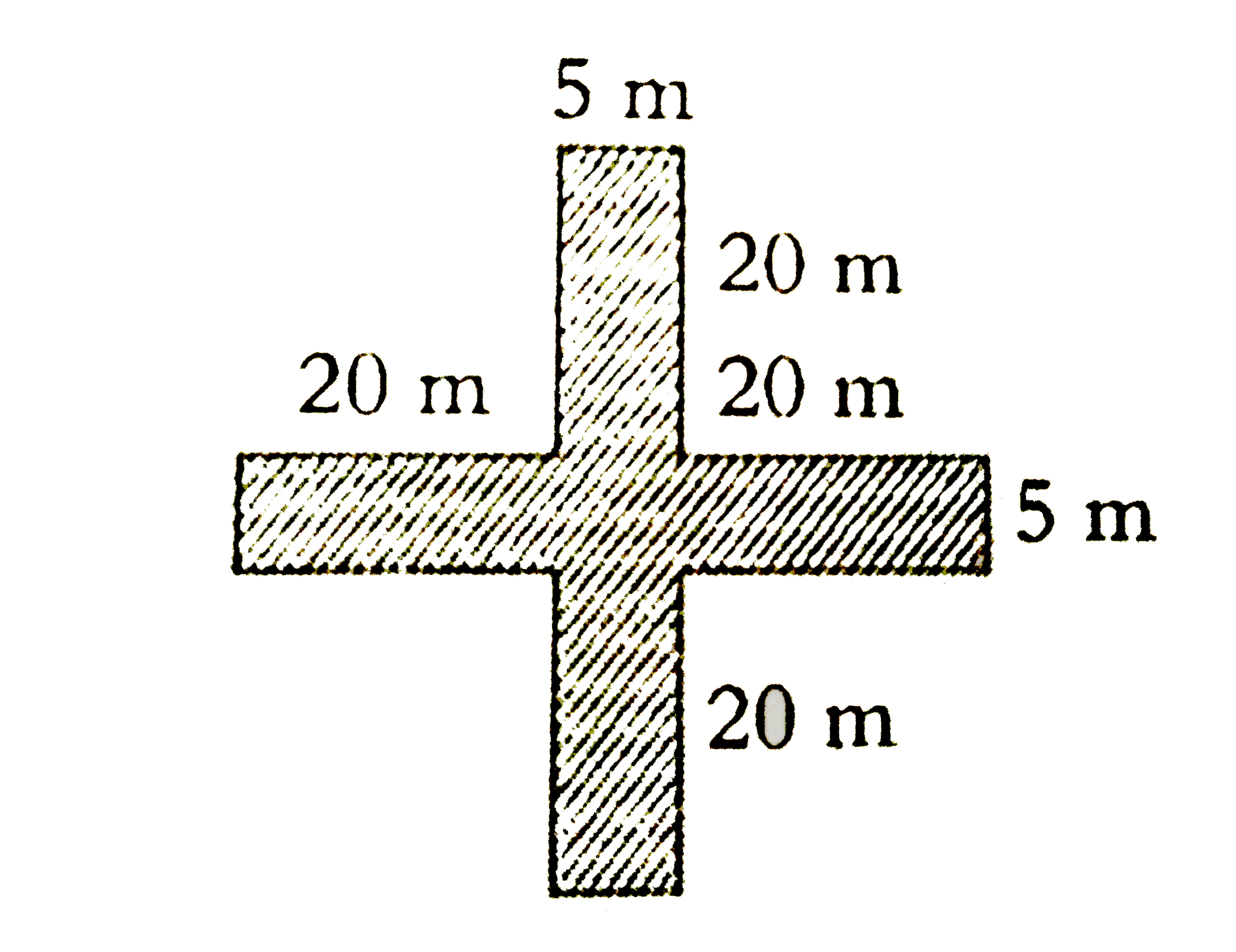
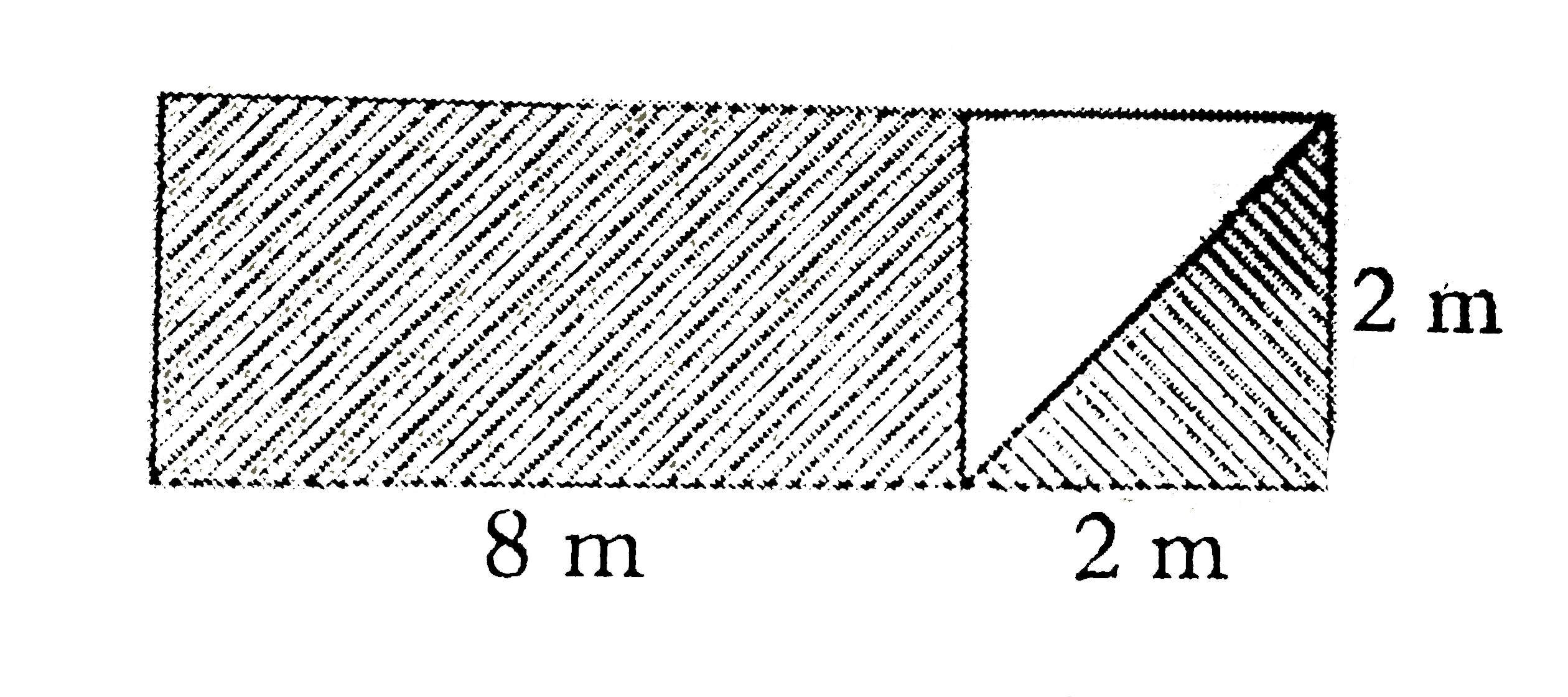
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solution

