DCIPD
IC C IP
PCICD
DICIP
The correct Answer is:D
To solve the question −CP−D−P−DC−I, we need to identify a pattern in the series and find the appropriate sequence that fits.
1. Identify the Elements: The given series consists of the elements: CP, D, P, DC, I. We notice that there are letters and dashes in the series.
2. Divide the Series: We can divide the series into parts based on the letters and dashes. We can see that there are four main components: C, D, P, and I. The dashes seem to represent gaps or placeholders.
3. Look for Patterns: We can observe that there are repeated letters in the series. The letters D, C, P, and I can be arranged in a sequence.
4. Establish the Sequence: By analyzing the letters, we can establish a sequence. The sequence appears to follow the order: D, C, P, I.
5. Fill in the Gaps: Now, we can fill in the gaps in the series based on the established sequence. The first element is D, the second is C, the third is P, and the fourth is I.
6. Determine the Missing Element: Since the series is cyclical and follows the order D, C, P, I, we can see that after I, the sequence would repeat starting with D. Thus, the missing element that fits in the first position is D.
7. Choose the Correct Option: Based on the established sequence and the missing element, we can conclude that the correct option to fill in the gap is D.
Final Answer:
The answer is option D.
The answer is option D.
Topper's Solved these Questions
- SERIES COMPLETION TEST Book:MCGROW HILL PUBLICATIONChapter:SERIES COMPLETION TEST Exercise:EXERCISE 3 TYPE III
Explore 10 Videos
- SERIES Book:MCGROW HILL PUBLICATIONChapter:SERIES Exercise:ILLUSTRATIVE EXAMPLES
Explore 3 Videos
- SITUATION REACTION TEST Book:MCGROW HILL PUBLICATIONChapter:SITUATION REACTION TEST Exercise:EXERCISE
Explore 15 Videos
Similar Questions
Knowledge Check
D : B : : I : C : : P : D : : ?
AU: EBX : ECY: DDZ : E
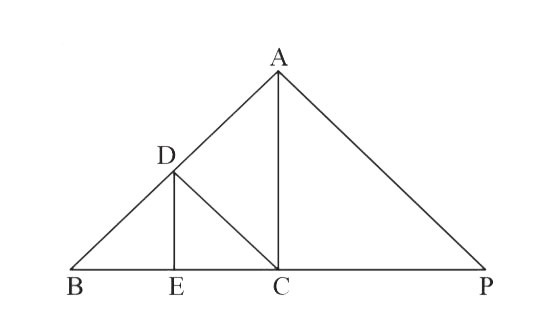
In the given figure DE || AC and BEEC=BCCP. Prove that DC || AP.
View SolutionDefine Cp and CV. Why is CP>CV ? For an ideal gas, prove that CP−CV=R .
View SolutionIf S.P. is ₹x, C.P. is ₹y and profit is z%. Then xy=………..
View SolutionIf C.P. = ₹ 100, S.P. = ₹ 90; then what is the percentage of loss ?
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).

View SolutionIn a □ABCD,AB∣∣DC. P and Q are the mid-points of ABandDC respectively AC,BD meet at O.Show that P,O,Q are collinear.
View SolutionGiven the following values, find the unknown values: (i) C.P. = Rs 1200, S.P. = Rs 1350 Profit/Loss=? (ii) C.P. = Rs 980, S.P. = Rs 940 Profit/Loss =?
View Solution
