1077 boxes of oranges were loaded in three trucks. While unloading them 7, 12 and 8 boxes were found rotten in the trucks respectively. If the number of remaining boxes in the three trucks are in the ratio 4:6: 5, find the number of boxes loaded originally in each truck
The correct Answer is:287, 432 and 358
To solve the problem, we need to find the number of boxes of oranges originally loaded in each of the three trucks, given the total number of boxes, the number of rotten boxes, and the ratio of the remaining boxes.
1. Identify the Total and Rotten Boxes:
- Total boxes loaded = 1077
- Rotten boxes in Truck A = 7
- Rotten boxes in Truck B = 12
- Rotten boxes in Truck C = 8
- Total rotten boxes = 7 + 12 + 8 = 27
2. Calculate Remaining Boxes:
- Remaining boxes = Total boxes - Rotten boxes
- Remaining boxes = 1077 - 27 = 1050
3. Set Up the Ratio of Remaining Boxes:
- The remaining boxes in the three trucks are in the ratio 4:6:5.
- Let the remaining boxes in Truck A, B, and C be represented as 4k, 6k, and 5k respectively.
4. Express Total Remaining Boxes in Terms of k:
- Total remaining boxes = 4k + 6k + 5k = 15k
- We know from step 2 that Total remaining boxes = 1050.
- Therefore, we can set up the equation: 15k = 1050.
5. Solve for k:
- k = 1050 / 15
- k = 70
6. Calculate Remaining Boxes in Each Truck:
- Remaining boxes in Truck A = 4k = 4 * 70 = 280
- Remaining boxes in Truck B = 6k = 6 * 70 = 420
- Remaining boxes in Truck C = 5k = 5 * 70 = 350
7. Find the Original Number of Boxes in Each Truck:
- Original boxes in Truck A = Remaining boxes + Rotten boxes = 280 + 7 = 287
- Original boxes in Truck B = Remaining boxes + Rotten boxes = 420 + 12 = 432
- Original boxes in Truck C = Remaining boxes + Rotten boxes = 350 + 8 = 358
Final Answer:
- Original boxes in Truck A = 287
- Original boxes in Truck B = 432
- Original boxes in Truck C = 358
- Total boxes loaded = 1077
- Rotten boxes in Truck A = 7
- Rotten boxes in Truck B = 12
- Rotten boxes in Truck C = 8
- Total rotten boxes = 7 + 12 + 8 = 27
- Remaining boxes = Total boxes - Rotten boxes
- Remaining boxes = 1077 - 27 = 1050
- The remaining boxes in the three trucks are in the ratio 4:6:5.
- Let the remaining boxes in Truck A, B, and C be represented as 4k, 6k, and 5k respectively.
- Total remaining boxes = 4k + 6k + 5k = 15k
- We know from step 2 that Total remaining boxes = 1050.
- Therefore, we can set up the equation: 15k = 1050.
- k = 1050 / 15
- k = 70
- Remaining boxes in Truck A = 4k = 4 * 70 = 280
- Remaining boxes in Truck B = 6k = 6 * 70 = 420
- Remaining boxes in Truck C = 5k = 5 * 70 = 350
- Original boxes in Truck A = Remaining boxes + Rotten boxes = 280 + 7 = 287
- Original boxes in Truck B = Remaining boxes + Rotten boxes = 420 + 12 = 432
- Original boxes in Truck C = Remaining boxes + Rotten boxes = 350 + 8 = 358
- Original boxes in Truck A = 287
- Original boxes in Truck B = 432
- Original boxes in Truck C = 358
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B52videos
MIXED PRACTICE
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (E)23videos
MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)
- BOOK - ICSECHAPTER - PROBABILITYEXERCISE - EXERCISE 25(C)106videos
PROBABILITY
Similar Questions
The mean of 7 numbers is 12, Four of the 7 numbers are 10,14,15, and 17. The remaining three numbers are in the ratio 1 : 2 : 4. Find these three numbers.
View SolutionFind the number of ways in which 5 distinct balls can be distributed in three different boxes if no box remains empty.
View Solution
Knowledge Check
- Question 1 - Select One
The most popular items at a bakery are its raspberry scones and its lemon poppy seed muffins. The shop sells both items in boxes of 12 at a cost of $15 per box of raspberry scones and $9 per box of lemon poppy seed muffins. On Friday and Saturday, the shop earned $396 by selliing a total of 46 boxes of these two items. If r and l represent the number of boxes of raspberry scones and lemon poppy seed muffins sold over the two-day period, respectively, which of the following systems of equations could be used to find the number of boxes of each type of item sold?
Ar+l=46
15r+9l=396Br+l=12×46
15r+9l=396Cr+l=46
15r+9l=3962Dr+l=12×46
15r+9l=39612 - Question 2 - Select One
To teach the chapter ratio and proportion in a class, the teacher asked the students of class X to make two groups of boys and girls to find the number of boys and girls. Class X has three sections A, B and C. The number of boys and girls in the three sections were found to be 24 and 32, 27 and 39 and 28 and 35, respectively.
What is the ratio of number of girls and boys in section C?A4:5B3:13C5:4D3:5 - Question 3 - Select One
To teach the chapter ratio and proportion in a class, the teacher asked the students of class X to make two groups of boys and girls to find the number of boys and girls. Class X has three sections A, B and C. The number of boys and girls in the three sections were found to be 24 and 32, 27 and 39 and 28 and 35, respectively.
What is the ratio of number of boys and girls in section B?A3:5B4:5C3:4D9:13
Raju wishes to put marbles in a small rectangular box in rows of 4 marbles each.
a. Find the rule that gives the number of marbles that can be put in the box.
b. Find the number of marbles if the number of rows is 7.View Solution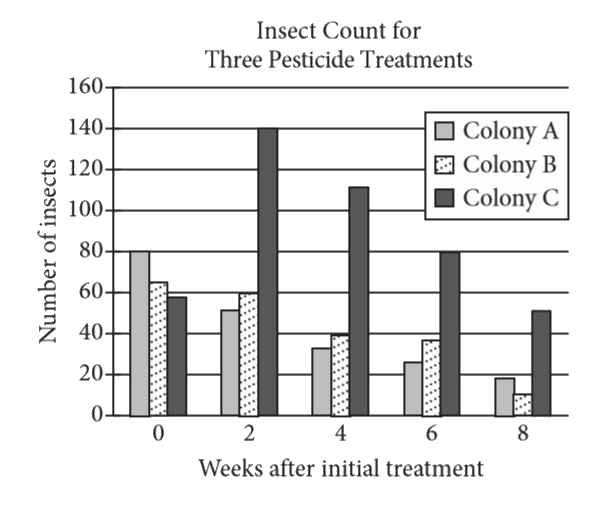
Three colonies of insects were each treated with a different pesticide over an 8-week period to test the effectiveness of the three pesticides. Colonies A, B, and C were treated with Pesticides A, B, and C, respectively. Each pesticide was applied every 2 weeks to one of the three colonies over the 8-week period. The bar graph above shows the insect counts for each of the three colonies 0, 2, 4, 6, and 8 weeks after the initial treatment.
Of the following, which is closest to the ratio of the total number of insects in all three colonies in week 8 to the total number of insects at the time of initial treatment?View SolutionA box contains 140 sweets. These sweets are divided amongst Rahul, Prateek, Arun, and Ashish in the ratio 2:3:4:5, respectively. Find the percentage of sweets received by each of the four friends. Also, find the number of sweets received by each friend.
View SolutionA box is placed on the floor of a truck moving with an acceleration of 7ms−2. If the coefficient of kinetic friction between the box and surface of the truck is 0.5, find the acceleration of the box relative to the truck
View SolutionTo teach the chapter ratio and proportion in a class, the teacher asked the students of class X to make two groups of boys and girls to find the number of boys and girls. Class X has three sections A, B and C. The number of boys and girls in the three sections were found to be 24 and 32, 27 and 39 and 28 and 35, respectively.
What is the ratio of number of boys and girls in section A?View Solution

