In a triangle PQR, L and M are two points on the base QR, such that and Prove that:
To prove that triangle PQL is similar to triangle RPM, we will use the Angle-Angle (AA) similarity criterion. Here are the steps to arrive at the solution:
Step 1: Identify the Given Angles
We are given:
- ∠LPQ=∠QRP
- ∠RPM=∠RQP
Step 2: Draw the Triangle
Draw triangle PQR with points L and M on the base QR. Mark the angles as given in the problem.
Step 3: State the Angles of Triangle PQL
From the given information, we can state:
- ∠LPQ=∠QRP (Given)
- ∠QPL=∠PRM (Since both angles are opposite to the equal angles in triangles)
Step 4: Find the Third Angles
Since the sum of angles in a triangle is 180 degrees, we can find the third angles:
- In triangle PQL, the third angle ∠PLQ can be expressed as:
∠PLQ=180∘−(∠LPQ+∠QPL)
- In triangle RPM, the third angle ∠RMP can be expressed as:
∠RMP=180∘−(∠RPM+∠PRM)
Step 5: Show that the Third Angles are Equal
Since ∠LPQ=∠QRP and ∠RPM=∠RQP, we can conclude:
- ∠PLQ=∠RMP
Step 6: Apply the AA Similarity Criterion
Now we have:
- ∠LPQ=∠QRP
- ∠QPL=∠PRM
- ∠PLQ=∠RMP
Since all three pairs of angles are equal, by the AA similarity criterion, we can conclude that:
△PQL∼△RPM
Conclusion
Thus, we have proved that triangle PQL is similar to triangle RPM.
---
We are given:
- ∠LPQ=∠QRP
- ∠RPM=∠RQP
Draw triangle PQR with points L and M on the base QR. Mark the angles as given in the problem.
From the given information, we can state:
- ∠LPQ=∠QRP (Given)
- ∠QPL=∠PRM (Since both angles are opposite to the equal angles in triangles)
Since the sum of angles in a triangle is 180 degrees, we can find the third angles:
- In triangle PQL, the third angle ∠PLQ can be expressed as:
∠PLQ=180∘−(∠LPQ+∠QPL)
- In triangle RPM, the third angle ∠RMP can be expressed as:
∠RMP=180∘−(∠RPM+∠PRM)
Since ∠LPQ=∠QRP and ∠RPM=∠RQP, we can conclude:
- ∠PLQ=∠RMP
Now we have:
- ∠LPQ=∠QRP
- ∠QPL=∠PRM
- ∠PLQ=∠RMP
△PQL∼△RPM
Thus, we have proved that triangle PQL is similar to triangle RPM.
Topper's Solved these Questions
- MIXED PRACTICE Book:ICSEChapter:MIXED PRACTICE Exercise:SET B
Explore 52 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)Book:ICSEChapter:MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)Exercise:EXERCISE 24 (E)
Explore 23 Videos
- PROBABILITYBook:ICSEChapter:PROBABILITYExercise:EXERCISE 25(C)
Explore 106 Videos
Similar Questions
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
PQ2=QR×QL
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
QL×RM=PL×PM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
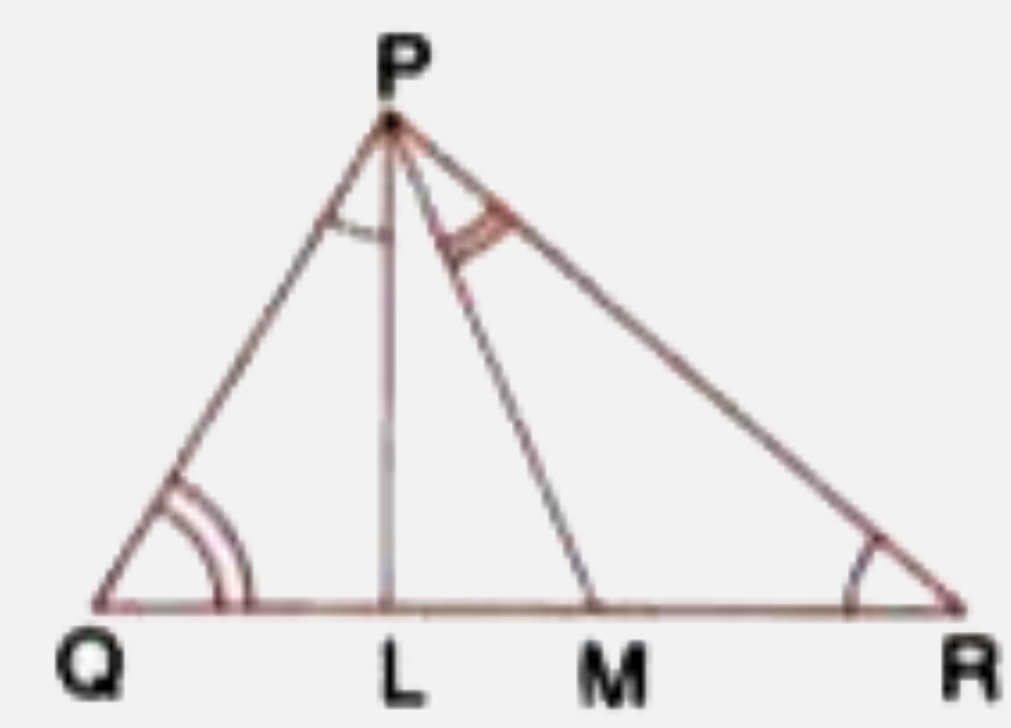
ΔPQL~ΔRPM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
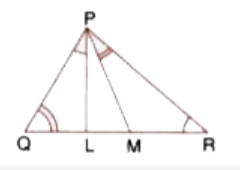
PQ2=QR×QL
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:

QL×RM=PL×PM
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
Prove that the triangles PTR and PSQ are congruent.
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
If OS and RT intersect at M, prove that the triangles PTM and PSM are congruent.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View SolutionIn the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
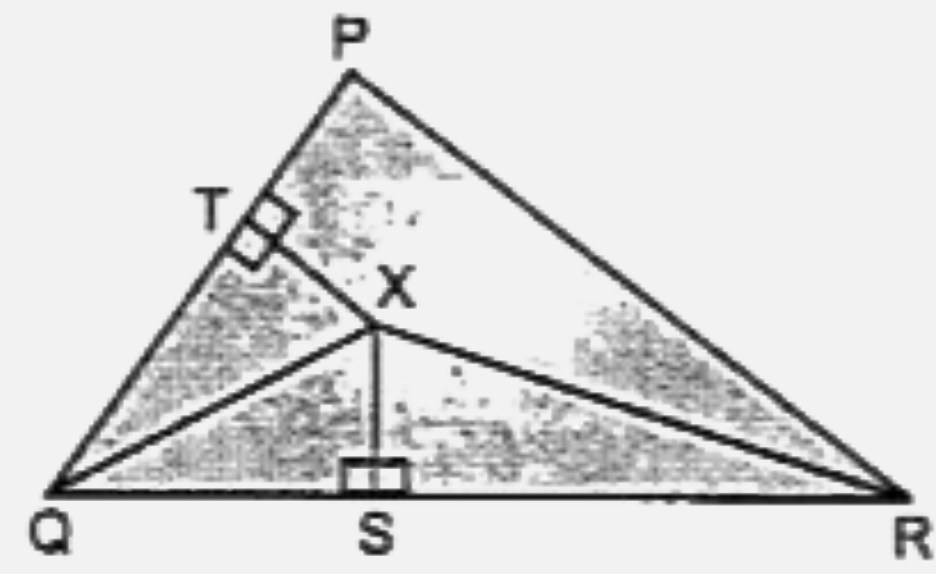
Prove that :
ΔXTQ≅ΔXSQ
View Solution