6 and −6 are at the same distance from 0 on the number line.
To determine if 6 and -6 are at the same distance from 0 on the number line, we can follow these steps:
Step 1: Draw a Number Line
- Start by drawing a horizontal line. This will represent the number line.
- Mark a point in the center of the line as 0.
Step 2: Mark Positive Integers
- To the right of 0, mark the positive integers at equal intervals. For example:
- 1, 2, 3, 4, 5, 6, and so on.
Step 3: Mark Negative Integers
- To the left of 0, mark the negative integers at equal intervals. For example:
- -1, -2, -3, -4, -5, -6, and so on.
Step 4: Measure the Distance from 0 to 6
- Count the intervals from 0 to 6:
- 0 to 1 (1), 1 to 2 (2), 2 to 3 (3), 3 to 4 (4), 4 to 5 (5), and 5 to 6 (6).
- The total distance from 0 to 6 is 6 units.
Step 5: Measure the Distance from 0 to -6
- Count the intervals from 0 to -6:
- 0 to -1 (1), -1 to -2 (2), -2 to -3 (3), -3 to -4 (4), -4 to -5 (5), and -5 to -6 (6).
- The total distance from 0 to -6 is also 6 units.
Conclusion
- Since both distances (from 0 to 6 and from 0 to -6) are equal to 6 units, we can conclude that 6 and -6 are indeed at the same distance from 0 on the number line.
---
- Start by drawing a horizontal line. This will represent the number line.
- Mark a point in the center of the line as 0.
- To the right of 0, mark the positive integers at equal intervals. For example:
- 1, 2, 3, 4, 5, 6, and so on.
- To the left of 0, mark the negative integers at equal intervals. For example:
- -1, -2, -3, -4, -5, -6, and so on.
- Count the intervals from 0 to 6:
- 0 to 1 (1), 1 to 2 (2), 2 to 3 (3), 3 to 4 (4), 4 to 5 (5), and 5 to 6 (6).
- The total distance from 0 to 6 is 6 units.
- Count the intervals from 0 to -6:
- 0 to -1 (1), -1 to -2 (2), -2 to -3 (3), -3 to -4 (4), -4 to -5 (5), and -5 to -6 (6).
- The total distance from 0 to -6 is also 6 units.
- Since both distances (from 0 to 6 and from 0 to -6) are equal to 6 units, we can conclude that 6 and -6 are indeed at the same distance from 0 on the number line.
Topper's Solved these Questions
- INTEGERS BOOK - NCERT EXEMPLARCHAPTER - INTEGERS EXERCISE - Exercise (Fill in the blanks to make the statements true:)
8 Videos
- INTEGERS BOOK - NCERT EXEMPLARCHAPTER - INTEGERS EXERCISE - Exercise (Fill in the blanks)
9 Videos
- INTEGERS BOOK - NCERT EXEMPLARCHAPTER - INTEGERS EXERCISE - Exercise (Only one of the four options is correct. Write the correct one.)
17 Videos
- GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise
56 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - Exercise (True or False)
7 Videos
Similar Questions
Knowledge Check
The absolute value of a number is its distance from 0 on a number line. The number line representing the inequaltiy |x|<4 is
A B
B C
C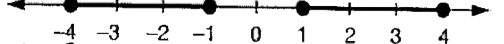 D
D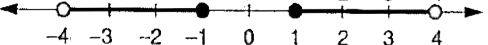
Represent the fractions on the number line.
67
View SolutionRepresent √6.3 on the number line .
View SolutionGraph the fraction on a number line.
56
View SolutionAdd −3 and −6 show on the number line.
View SolutionRepresent 1+6 using the number line.
View SolutionFind the distance from the origin to (6,6,7).
View SolutionThere are 15 points in a plane, no three of which are in the same straight line with the exception of 6, which are all in the same straight line. Find the number of i. straight lines formed, ii. number of triangles formed by joining these points.
View Solution
