A (−1,0)andB(2,0) are two given points. A point M is moving in such a way thatthe angle B in the triangle AMB remains twice as large as the angle A. Show that the locus of the pointM is a hyperbola. Find the eccentricity of the hyperbola.
a straight line
a parabola
an ellipse
a hyperbola
The correct Answer is:D
Step by step video, text & image solution for A (-1, 0) and B (2, 0) are two given points. A point M is moving in such a way thatthe angle B in the triangle AMB remains twice as large as the angle A. Show that the locus of the pointM is a hyperbola. Find the eccentricity of the hyperbola. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- STRAIGHT LINESBOOK - MTG-WBJEECHAPTER - STRAIGHT LINESEXERCISE - WB JEE Previous Years Questions
28 Videos
- STATISTICS AND PROBABILITYBOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE Previous Years Questions ( CATEGORY 3 : One or More than One Option Correct Type ( 2 Marks) )
3 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - MTG-WBJEECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - WE JEE PREVIOUS YEARS QUESTIONS (CATEGORY 1 : Single Option Correct Type)
10 Videos
Similar Questions
Knowledge Check
A and B are two fixed points. The locus of a point P such that ∠APB is a right angle, is:
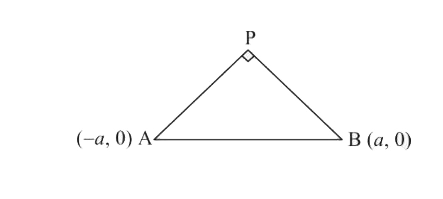 Ax2+y2=a2Bx2−y2=a2C2x2+y2=a2DNone of these
Ax2+y2=a2Bx2−y2=a2C2x2+y2=a2DNone of these
If AOBandCOD are two straight lines which bisect one another at right angles, show that the locus of a points P which moves so that PAxPB=PCxPD is a hyperbola. Find its eccentricity.
View SolutionProve that the locus of a point, tangents from where to hyperbola x2−y2=a2 inclined at an angle α&β with x-axis such that tanαtanβ=2 is also a hyperbola. Find the eccentricity of this hyperbola.
View SolutionA(0,0),B(1,2) are two points. If a point P moves such that the area of ΔPAB is 2 sq. units then the locus of P is
View SolutionGiven the base of a triangle and the ratio of the tangent of half the base angles .Show that the vertex moves on a hyperbola whose foci are the extremities of a diameter
View SolutionTwo straight lines pass through the fixed points (±a,0) and have slopes whose products is p>0 Show that the locus of the points of intersection of the lines is a hyperbola.
View SolutionThe tangent at P on the hyperbola x2a2−y2b2=1 meets one of the asymptote in Q. Show that the locus of the mid point of PQ is a similar hyperbola.
View SolutionThere are two points A(a,0)andB(−a,0) . If ∠A−∠B=θ then the locus of C in the triangle ABC is
View Solution
