If $A O B a n d C O D$ are two straight lines which bisect one another at right angles, show that the locus of a points $P$ which moves so that $P A x P B = P C x P D$ is a hyperbola. Find its eccentricity.

Video Solution

Answer

Step by step video & image solution for If A O Ba n dC O D are two straight lines which bisect one another at right angles, show that the locus of a points P which moves so that P AxP B=P CxP D is a hyperbola. Find its eccentricity. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS PARABOLA

Knowledge Check

A and B are two fixed points. The locus of a point P such that $∠ A P B$ is a right angle, is:

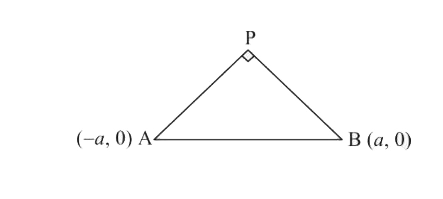A $x^{2} + y^{2} = a^{2}$
B $x^{2} - y^{2} = a^{2}$
C $2 x^{2} + y^{2} = a^{2}$
DNone of these

If $A$ and $B$ are two fixed points, then the locus of a point which moves in such a way that the angle $A P B$ is a right angle is
View Solution
Two straight lines pass through the fixed points $(\pm a, 0)$ and have slopes whose products is $p > 0$ Show that the locus of the points of intersection of the lines is a hyperbola.
View Solution
A and B are two fixed points and the line segment AB always subtends an acute angle at a variable point P. Show that the locus of the point P is a circle.
View Solution
If a bar of givenlength moves with its extremities on two fixed straight lines at right angles,then the locus of any point on bar marked on the bar describes a/an :
View Solution
A point P moves such that its distances from two given points A and B are equal. Then what is the locus of the point P ?
View Solution
The line join of the points $(2, 3)$ and $(- 1, 5)$ subtends a right angle at $P$ . If the locus of $P$ is a circle then its radius is
View Solution
The normal at $P$ to a hyperbola of eccentricity $e$ , intersects its transverse and conjugate axes at $L$ and $M$ respectively. Show that the locus of the middle point of $L M$ is a hyperbola of eccentricity $\frac{e}{\sqrt{e^{2} - 1}}$
View Solution

If $A O B a n d C O D$ are two straight lines which bisect one another at right angles, show that the locus of a points $P$ which moves so that $P A x P B = P C x P D$ is a hyperbola. Find its eccentricity.

Similar Questions

Knowledge Check

A and B are two fixed points. The locus of a point P such that $∠ A P B$ is a right angle, is:

Recommended Questions

If AOBandCOD are two straight lines which bisect one another at right angles, show that the locus of a points P which moves so that PAxPB=PCxPD is a hyperbola. Find its eccentricity.

Similar Questions

Knowledge Check

A and B are two fixed points. The locus of a point P such that ∠APB is a right angle, is:

Recommended Questions

If $A O B a n d C O D$ are two straight lines which bisect one another at right angles, show that the locus of a points $P$ which moves so that $P A x P B = P C x P D$ is a hyperbola. Find its eccentricity.

A and B are two fixed points. The locus of a point P such that $∠ A P B$ is a right angle, is: