AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB=350, then ∠CFQ will be 550 (b) 700 (c) 1100 (d) 1300
"Given that,
'AB || CD' and 'PQ' cuts them
'EL' is bisector of '/_FEB'
'/_LEB= /_FEL= 35@'
'/_FEB = /_LEB + /_FEL'
= '35@ + 35@'
= '70@'
'/_FEB =/_EFC = = 70@'(Alternate angles)
'/_EFC + /_CFQ = 180@'(Linear pair)
'70@ + /_CFQ=180@'
'/_CFQ=110@'"
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC=35∘ , then ∠ABC= 70∘ (b) 110∘ (c) 90∘ (d) 120∘
View SolutionIn ABC, ∠B=∠C and ray AX bisects the exterior angle ∠DAC.If ∠DAX=700, then ∠ACB= 350 (b) 900 (c) 700 (d) 550
View SolutionIn Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= 1000 (b) 800 (c) 900 (d) 1350
View SolutionIn Figure, if EC∣∣AB, ∠ECD=700AND ∠BDO=200 , then ∠OBD is: 200 (b) 500 (c) 600 (d) 700
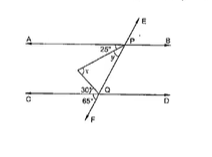
View SolutionIn Figure, AB and CD are parallel lines and transversal EF intersects them at P and Q respectively. If ∠APR=250, ∠RQC=300and ∠CQF=650, then x=550, y=440 (b) x=550, y=450 x=600, y=350 (d) x=350, y=600
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View Solution
