A, B, C, D are four points in the space and satisfy |vec(AB)|=3, |vec(

Assertion A : If A, B, C, D are four points on a semi-circular arc with centre at 'O' such that
$∣ ∣ ∣ - - \to A B ∣ ∣ ∣ = ∣ ∣ ∣ - - \to B C ∣ ∣ ∣ = ∣ ∣ ∣ - - \to C D ∣ ∣ ∣$ , then
$- - \to A B + - - \to A C + - - \to A D = 4 - - \to A O + - - \to O B + - - \to O C$
Reason R : Polygon law of vector addition yields
$- - \to A B + - - \to B C + - - \to C D + - - \to A D = 2 - - \to A O$

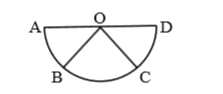
In the light of the above statements, choose the most appropriate answer from the options given below :
AA is correct but R is not correct.
BA is not correct but R is correct.
CBoth A and R are correct and R is the correct explanation of A.
DBoth A and R are correct but R is not the correct explanation of A.
If A, B, C and D are four points in space having $∣ ∣ ∣ - - \to A B \times - - \to C D + - - \to B C \times - - \to A D + - - \to C A \times - - \to B D ∣ ∣ ∣$ , then the value = k (Area of $△ A B C$ ) of k is equal to
A4
B3
C2
D5
If $| \to a | = 7, ∣ ∣ \to b ∣ ∣ = 11 and ∣ ∣ \to a + \to b ∣ ∣ = 10 \sqrt{3}$ , then $∣ ∣ \to a - \to b ∣ ∣$ is equal to
A40
B10
C $4 \sqrt{10}$
D $2 \sqrt{10}$

A, B, C, D are four points in the space and satisfy $∣ ∣ ∣ - - \to A B ∣ ∣ ∣ = 3, ∣ ∣ ∣ - - \to B C ∣ ∣ ∣ = 7, ∣ ∣ ∣ - - \to C D ∣ ∣ ∣ = 11 and ∣ ∣ ∣ - - \to D A ∣ ∣ ∣ = 9$ . Then find the value of $- - \to A C \cdot - - \to B D$ .