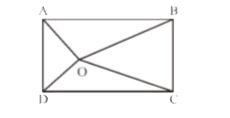
Let OA, OB, OC be coterminous edges of a cubboid. If l, m, n be the shortest distances between the sides OA, OB, OC and their respective skew body diagonals to them, respectively, then find (1l2+1m2+1n2)(1OA2+1OB2+1OC2).
The correct Answer is:2
Topper's Solved these Questions
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-4 : Matching Type Problems
1 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
Knowledge Check
If OA=a, OB=b, OC=c are the co-terminus edges of regular parallelopiped, then the shortest distance between the diagonal and the side OB not meeting the diagonal is
Abc√b2+c2Bca√c2+a2Cab√a2+b2Dabc√a2+b2+c2If OA=a, OB=b, OC=c are the co-terminus edges of regular parallelopiped, then the shortest distance between the diagonal and the side OA not meeting the diagonal is
Abc√b2+c2Bca√c2+a2Cab√a2+b2Dabc√a2+b2+c2
Point A and B are in the first quadrant; point O is the origin. If the slope of OA is 1, the slope of OB is 7, and OA=OB, then the slope of AB is −15 (b) −14 (c) −13 (d) −12
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC ?
View SolutionIn a tetrahedron OABC, if OA=ˆi,OB=ˆi+ˆjandOC=ˆi+2ˆj+ˆk,if shortest distance between egdes OA and BC is m, then √2m is equal to …(where O is the origin).
View SolutionIn a tetrahedron OABC, if OA=ˆi,OB=ˆi+ˆjandOC=ˆi+2ˆj+ˆk,if shortest distance between egdes OA and BC is m, then √2m is equal to …(where O is the origin).
View SolutionA(1,−2)andB(2,5) are two points. The line OA, OB are produced to C and D respectively such that OC=2OAandOD=20B. Find CD
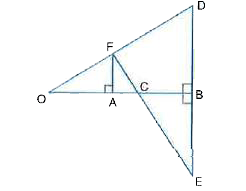
View SolutionIn the Fig. given below, OB is the perpendicular bisector of the line segment DE, FA⊥OB and FE intersects OB at the point C. Prove that 1OA+1OB=2OC
View Solution