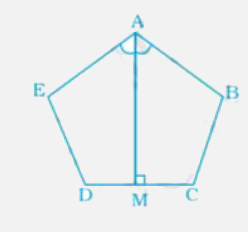
$A B C D E$ is a regular pentagon. The bisector of $∠ A$ of the pentagon meets the side $C D$ in $M$ Show that $∠ A M C = 90^{\circ}$ In pentagon $A B C D E$

Video Solution

Text Solution

Verified by Experts

In $A B C D E$ pentagon
interior angle $= (5 - 2) \times \frac{180^{0}}{5}$
$= 108^{0}$
in $A B C M$ by angle sum
$∠ B + ∠ C + ∠ B A M + ∠ A M C = 360^{0}$
$108^{0} + 108^{0} + 54^{0} + ∠ A M C = 360^{0}$
$∠ A M C = 90^{0}$

|

Updated on:21/07/2023

Class 8 MATHS VISUALISING SOLID SHAPES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABCDE is a regular pentagon. Angle bisector of $∠ B A E$ meets CD at m. angle bisector of $∠ B C D$ meets AM at P. Find the $∠ C P M$ = ?
A30
B35
C36
D60
Question 2 - Select One
ABCDE is a regular pentagon with sides of length 6 cm. CD is also a side of a regular polygon with n sides. Given that $∠ E D F = 90^{\circ}$ , find n.

A $18^{\circ}$
B $10^{\circ}$
C $20^{\circ}$
D $12^{\circ}$

RD SHARMA-UNDERSTANDING PHASE-II (QUADRILATERALS)-All Questions

Home
Ask Doubt
Profile