ABCD is a flower bed. If OA=21 m and OC=14 m , find the area of the bed. (Take π=22/7)
Step by step video & image solution for A B C D is a flower bed. If O A=21\ m and O C=14\ m , find the area of the bed. (T a k e\ \ pi=22//7) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
ABCD is a flower bed. If OA=21 m and OC=14 m , find the area of the bed. (Take π=22/7)
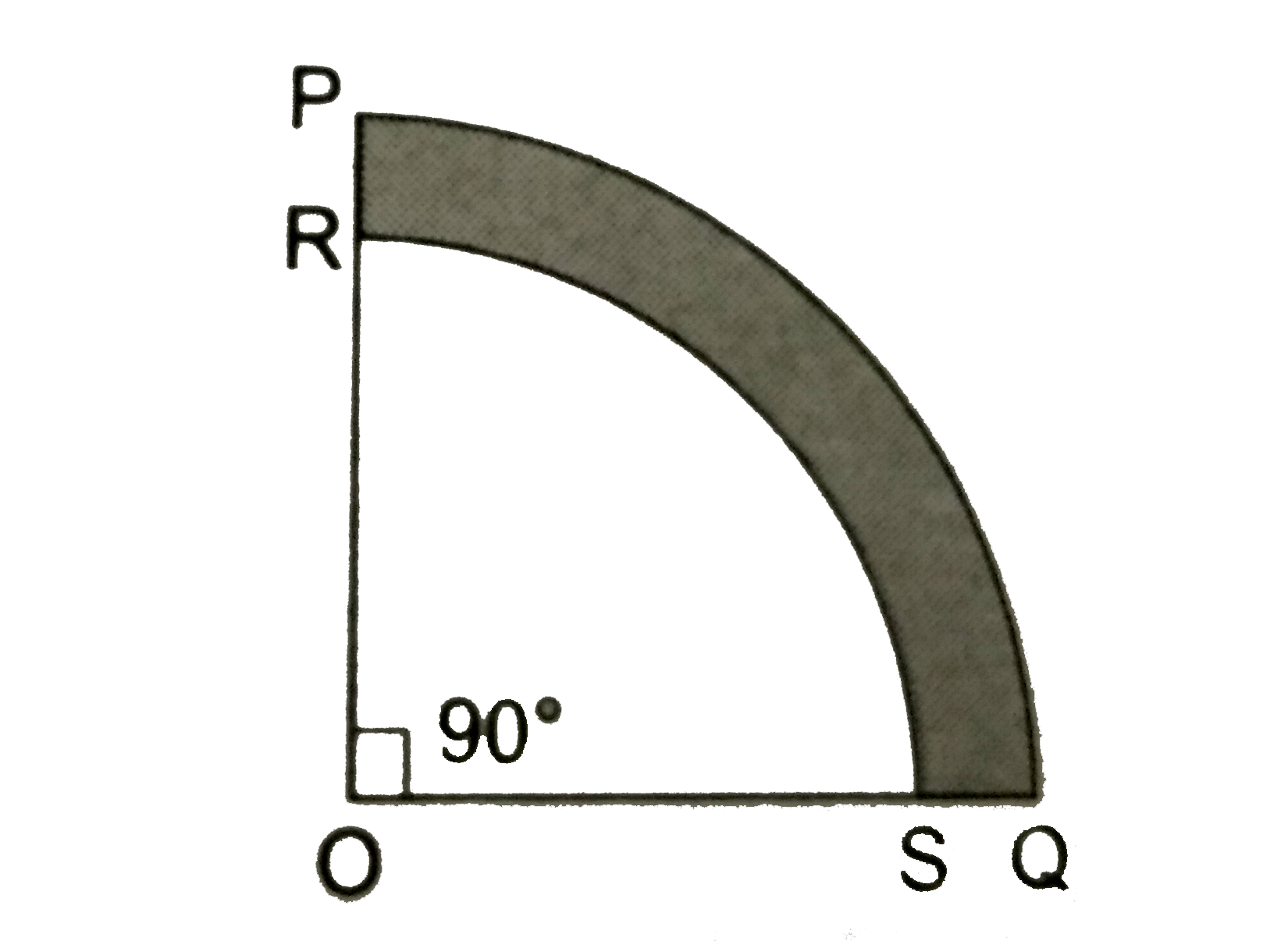
View SolutionIn the given figure, PQSR represents a flower bed. If OP=21m and OR=14m, find the area of the flower bed.
 View Solution
View SolutionIn Fig. 15.101, ABCD is a trapezium of area 24.5 cm2 . In it, ADBC , ∠DAB=90o , AD=10 cm and BC=4 cm . If ABE is a quadrant of a circle, find the area of the shaded region. (Take π=22/7) . (FIGURE)
View SolutionIn Fig. 15.72 (a) , OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O , then find the area of the shaded region. (Use π=22/7) (FIGURE)
View SolutionIn Fig. 15.63, ABCD is a trapezium with ABDC and ∠BCD=60o . If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4 cm , then find the area of the shaded region (Use π=227 and √3=1.732) .
View SolutionTwo circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm×7 cm . Find the area of the remaining card board. (Use π=22/7)
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Fig. 15.69, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region. (FIGURE)
View SolutionTriangles ABC and DEF are similar. If area (ABC)=36 cm2 , area (DEF)=64 cm2 and DE=6.2cm, find AB. (ii) If AB=1.2cm and DE=1.4cm , find the ratio of the areas of ABC and DEF .
View SolutionIn Fig. 15.103, from a rectangular region ABCD with AB=20 cm , a right triangle AED with AE=9 cm and DE=12cm , is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. (Use π=22/7)
View Solution

