$A B C$ is an equilateral triangle with $A (0, 0)$ and $B (a, 0)$ , (a>0). L, M and $N$ are the foot of the perpendiculars drawn from a point $P$ to the side $A B, B C, a n d C A$ , respectively. If $P$ lies inside the triangle and satisfies the condition $P L^{2} = P M . P N,$ then find the locus of $P .$

Video Solution

Text Solution

Verified by Experts

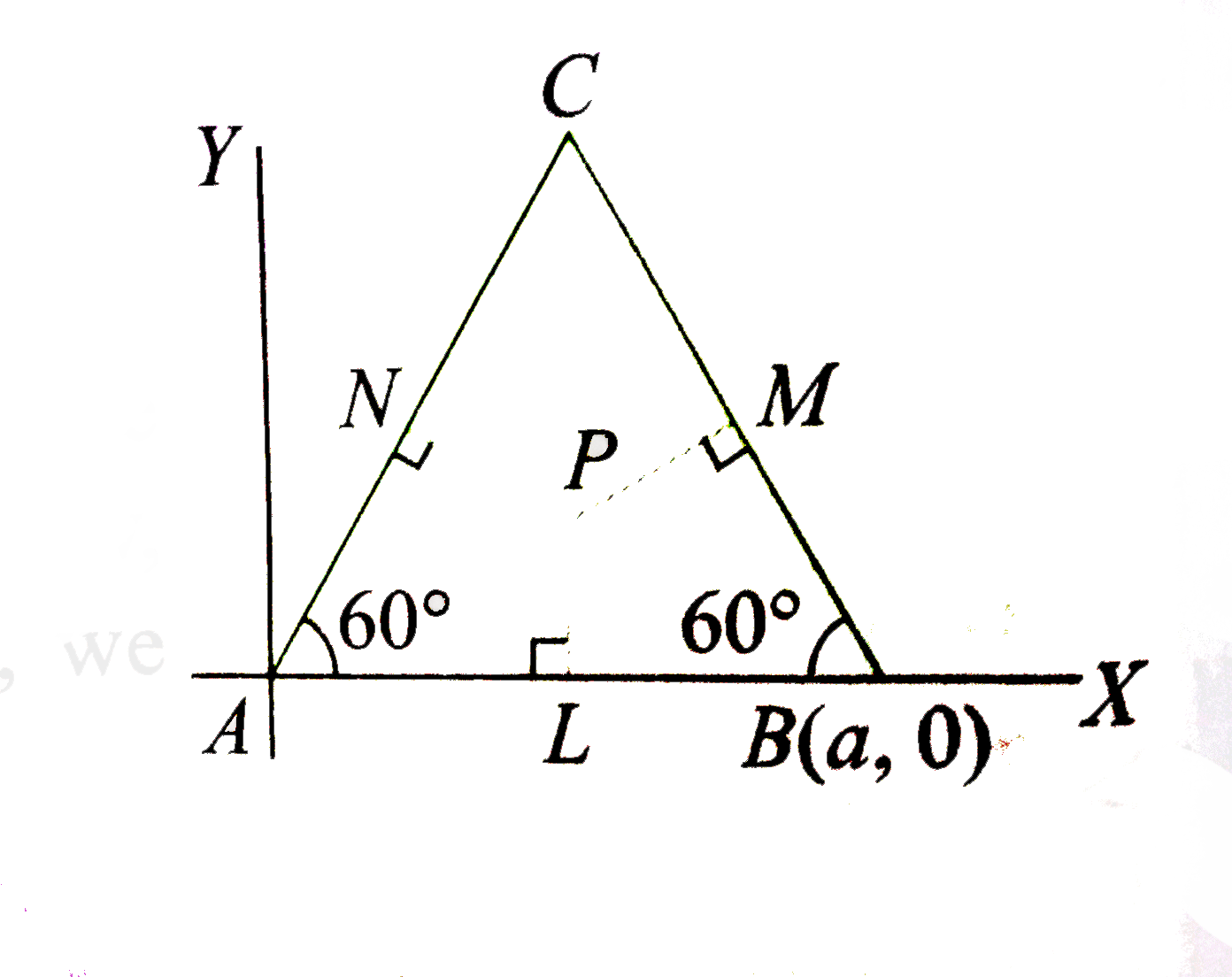
The equations of lines AC and BC are, respectively, given by
$y - \sqrt{3} x = 0$
$y + \sqrt{3} (x - a) = 0$
Let P(h,k) be the coordinates of the point whose locus is to be found. Now, according to the given condition, we have
$P L^{2} = P M \cdot P N$
$i . e ., k^{2} = \frac{∣ ∣ k - \sqrt{3} h ∣ ∣}{2} \cdot \frac{∣ ∣ k + \sqrt{3} (h - a) ∣ ∣}{2}$
$i . e ., 4 k^{2} = (k - \sqrt{3} h) [k + \sqrt{3} (h - a)] [∵ P lies below both the lines]$
$i . e ., 3 (h^{2} + k^{2}) - 3 a h + \sqrt{3} a k = 0$
$i . e ., h^{2} + k^{2} - a h + \frac{a}{\sqrt{3}} k = 0$
Putting (x,y) in place of (h,k) gives the equation of the required locus as
$x^{2} + y^{2} - a x + \frac{a}{\sqrt{3}} y = 0$

Updated on:21/07/2023