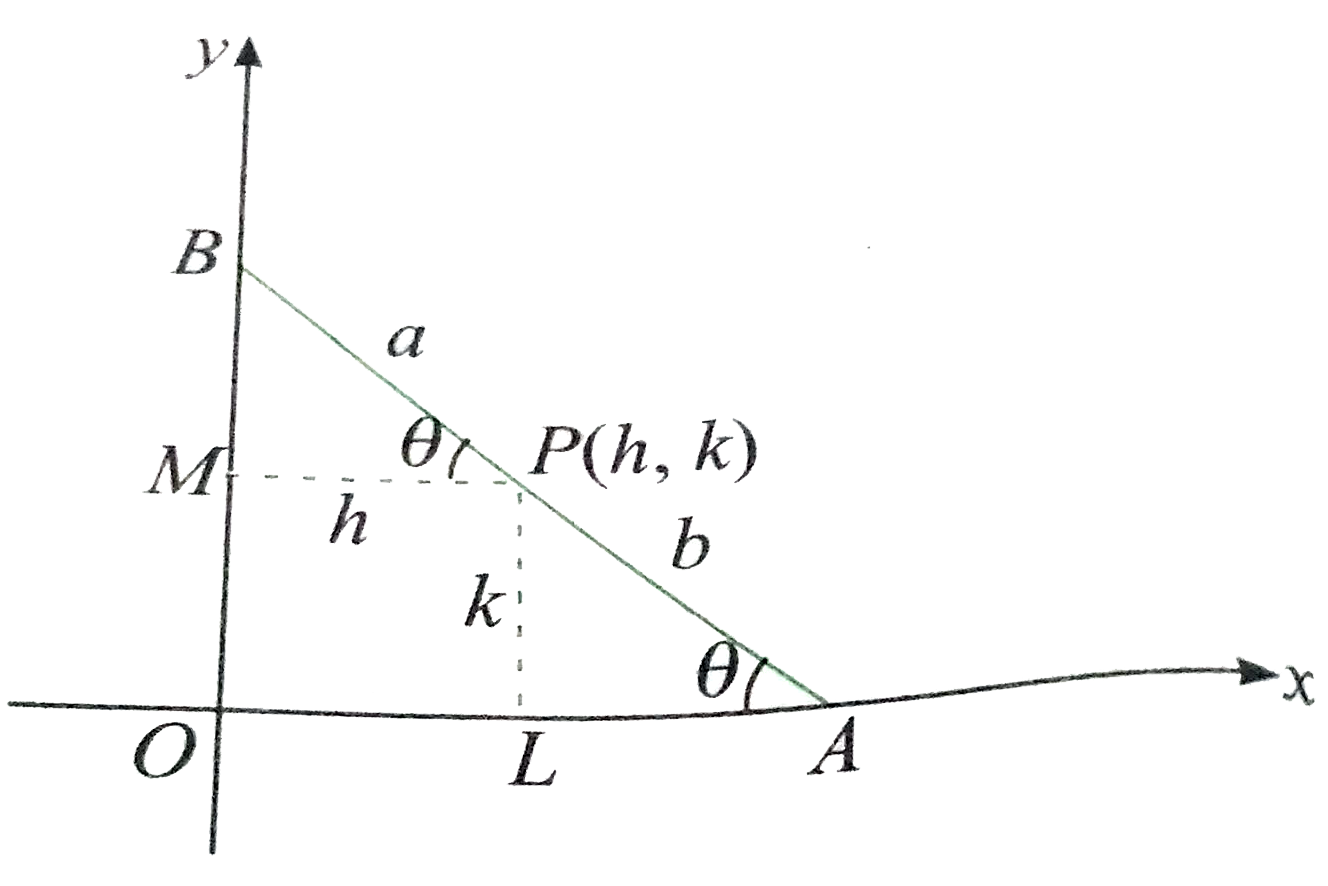
$A B$ is a variable line sliding between the coordinate axes in such a way that $A$ lies on the x-axis and $B$ lies on the y-axis. If $P$ is a variable point on $A B$ such that $P A = b, P b = a$ , and $A B = a + b,$ find the equation of the locus of $P .$

Video Solution

Text Solution

Verified by Experts

Let $P (h, k)$ be a variable point on AB such that $∠ O A B = θ$ .
Here, $θ$ is a variable from triangles ALP and PMB.we have
$sin θ = \frac{k}{b}$ (1)
$cos θ = \frac{h}{a}$ (2)
Here, $θ$ is a variable so, we have to elimiante $θ$ . Squareing (1) and (2) and adding, we get
$\frac{k^{2}}{b^{2}} + \frac{h^{2}}{a^{2}} = 1$
$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a $Δ A B C$ vertex A and B lies on 2 - axis and y -axis respectively, where A(a,0) is a fixed point, B is a variable point such that $∠ C = \frac{{tan}^{- 1} 4}{3}$ and AC = BC, then locus of C
A $2 x - 4 y + 3 a = 0$
B $4 x + 2 y - 3 a = 0$
C $2 x + 4 y + 7 a = 0$
D $4 x - 2 y + 5 a = 0$
Question 2 - Select One
If the mid point between the points $(a + b, a - b)$ and $(- a, b)$ lies on the line $a x + b y = k$ , what is k equal to ?
A $a / b$
B $a + b$
C $a b$
D $a - b$
Question 3 - Select One
A variable line passes through a fixed point (a,b) and meets the coordinate axes in A and B. The locus of the point of intersection of lines through A, B parallel to coordinate axes is
A $\frac{x}{a} + \frac{y}{b} = 1$
B $\frac{a}{x} + \frac{b}{y} = 1$
C $\frac{x}{a} + \frac{y}{b} = 2$
D $\frac{x}{a} + \frac{y}{b} = 3$

CENGAGE-COORDINATE SYSYEM -JEE Main Previous Year

Home
Ask Doubt
Profile