Question

A balloon of radius r subtends an angle${\displaystyle \alpha }$ at the eyes of an observer and the center of balloon from the eye is ${\displaystyle \beta }$ . Find the height of the center of the balloon from the eye of observer .

Explanation

Let O be the centre of the balloon of radius which subtends an angle` alpha` at E , the eyes of observer .

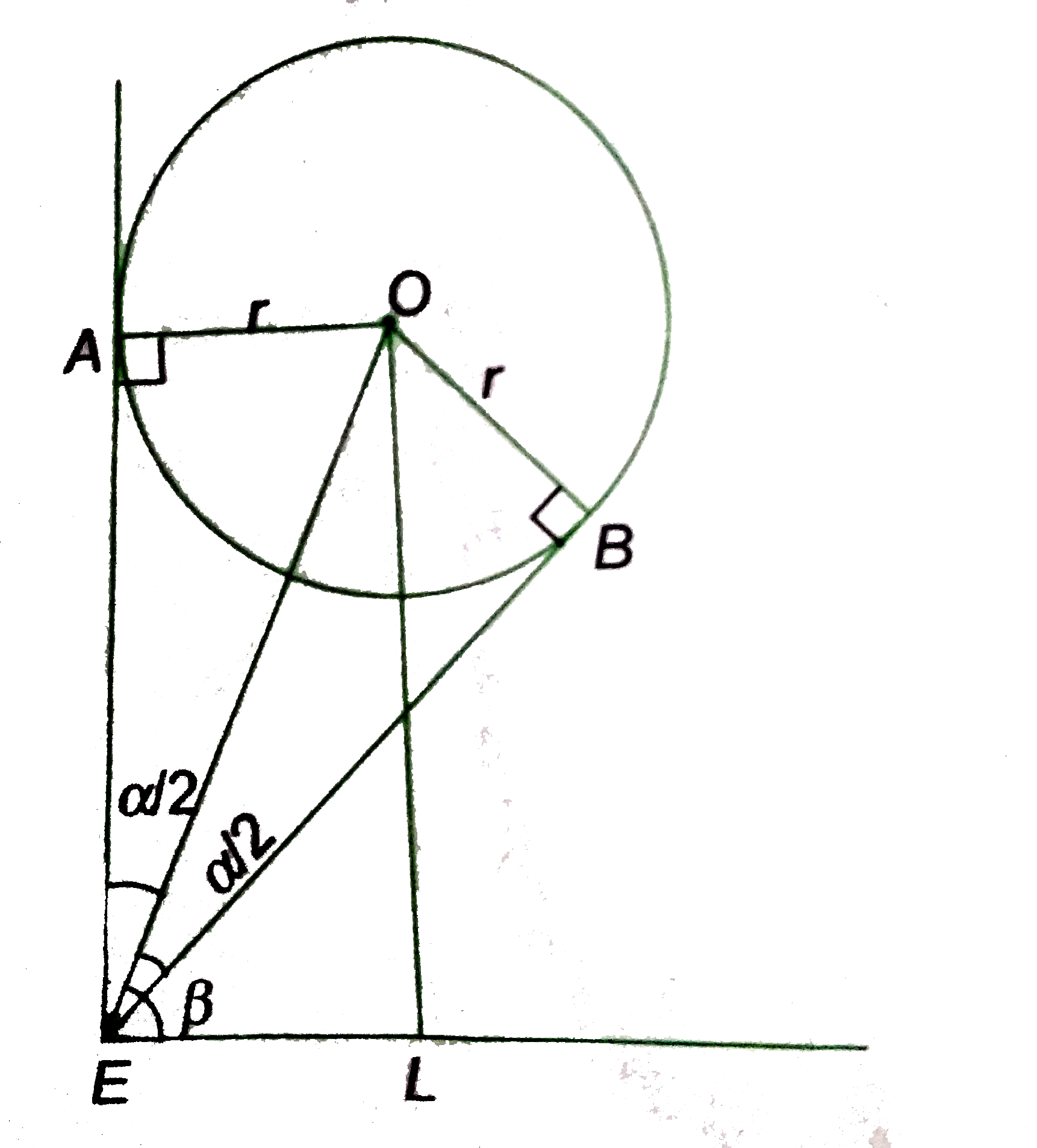
EA and EB are the tangents to the balloon .
`therefore angle OEA = angle OEB =alpha//2`
Let the height OL of the balloon be h .
In `Delta` OLE ,
h=OE sinbeta
`= rcosec(alpha//2)sinbeta` ( in triangle OBE)
`=(rsinbeta)/(sin(alpha//2))`