A bead shop sell wooden beads for $0.20 each and crystal beads for $0.50 each. If a jewelry artist buys 127 beads total and pays $41 for them, how much more did she spend on crystal beads than wooden beads ?
$11
$15
$23
$26
The correct Answer is:A
To solve the problem step by step, we will set up a system of equations based on the information given.
Step 1: Define Variables
Let:
- c = number of crystal beads
- w = number of wooden beads
Step 2: Set Up the Equations
From the problem, we know:
1. The total number of beads is 127:
c+w=127(Equation 1)
2. The total cost of the beads is $41. The cost of wooden beads is $0.20 each and the cost of crystal beads is $0.50 each:
0.20w+0.50c=41(Equation 2)
Step 3: Simplify Equation 2
To eliminate the decimals, we can multiply Equation 2 by 10:
2w+5c=410(Equation 3)
Step 4: Solve the System of Equations
Now we have the following system of equations:
1. c+w=127
2. 2w+5c=410
From Equation 1, we can express w in terms of c:
w=127−c
Step 5: Substitute w in Equation 3
Now substitute w in Equation 3:
2(127−c)+5c=410
Expanding this gives:
254−2c+5c=410
Combine like terms:
3c+254=410
Step 6: Solve for c
Subtract 254 from both sides:
3c=410−254
3c=156
Divide by 3:
c=52
Step 7: Find w
Now substitute c back into the equation for w:
w=127−52=75
Step 8: Calculate the Total Cost for Each Type of Bead
Now we can find out how much was spent on each type of bead:
- Cost of crystal beads:
Cost of crystal beads=0.50×c=0.50×52=26
- Cost of wooden beads:
Cost of wooden beads=0.20×w=0.20×75=15
Step 9: Find the Difference in Spending
To find out how much more was spent on crystal beads than wooden beads:
Difference=Cost of crystal beads−Cost of wooden beads=26−15=11
Final Answer
The jewelry artist spent $11 more on crystal beads than on wooden beads.
---
Let:
- c = number of crystal beads
- w = number of wooden beads
From the problem, we know:
1. The total number of beads is 127:
c+w=127(Equation 1)
0.20w+0.50c=41(Equation 2)
To eliminate the decimals, we can multiply Equation 2 by 10:
2w+5c=410(Equation 3)
Now we have the following system of equations:
1. c+w=127
2. 2w+5c=410
w=127−c
Now substitute w in Equation 3:
2(127−c)+5c=410
Expanding this gives:
254−2c+5c=410
Combine like terms:
3c+254=410
Subtract 254 from both sides:
3c=410−254
3c=156
Divide by 3:
c=52
Now substitute c back into the equation for w:
w=127−52=75
Now we can find out how much was spent on each type of bead:
- Cost of crystal beads:
Cost of crystal beads=0.50×c=0.50×52=26
- Cost of wooden beads:
Cost of wooden beads=0.20×w=0.20×75=15
To find out how much more was spent on crystal beads than wooden beads:
Difference=Cost of crystal beads−Cost of wooden beads=26−15=11
The jewelry artist spent $11 more on crystal beads than on wooden beads.
Topper's Solved these Questions
- SYSTEMS OF LINEAR EQUATIONSBOOK - KAPLANCHAPTER - SYSTEMS OF LINEAR EQUATIONSEXERCISE - SUBSTITUTION
1 Videos
- SYSTEMS OF LINEAR EQUATIONSBOOK - KAPLANCHAPTER - SYSTEMS OF LINEAR EQUATIONSEXERCISE - COMBINATION
1 Videos
- SYSTEMS OF LINEAR EQUATIONSBOOK - KAPLANCHAPTER - SYSTEMS OF LINEAR EQUATIONSEXERCISE - ON TEST DAY
1 Videos
- SCATTERPLOTSBOOK - KAPLANCHAPTER - SCATTERPLOTSEXERCISE - SCATTERPLOT MODELING
1 Videos
- THE MATHOD OF SAT MATH QUESTIONS BOOK - KAPLANCHAPTER - THE MATHOD OF SAT MATH QUESTIONS EXERCISE - TRY ON YOUR OWN
10 Videos
Similar Questions
Knowledge Check
Carrie's Chocolate shop and Tamika's Treat Shop both sell cadny in boxes. The table below lists the price (the total amount the customer pays) of each box of candy sold at the shops. For each shop, there is a linear relationship between the price of a box of candies and the number of candies in the box. These are the only numbers of candies that can be purchased at the shops.

Jeremy has $ 10.00 in quarters to spend on candy. What is the maximum number of quarters he would have left after paying for a box 25 candies at Tamika's treat Shop?
(Note: Each quarter is worth $ 0.25)A10B17C22D23Carrie's Chocolate shop and Tamika's Treat Shop both sell cadny in boxes. The table below lists the price (the total amount the customer pays) of each box of candy sold at the shops. For each shop, there is a linear relationship between the price of a box of candies and the number of candies in the box. These are the only numbers of candies that can be purchased at the shops.

At Tamika's Treat Shop. What is the average price per candy in a box of 20, to the nearest $0.01 ?A$0.08B$0.19C$0.23D$0.30Every day, millions of shoppers hit the stores in
full force—both online and on foot—searching
frantically for the perfect gift. Last year, Americans
spent over $30 billion at retail stores in the month of
5 December alone. Aside from purchasing holiday
gifts, most people regularly buy presents for other
occasions throughout the year, including weddings,
birthdays, anniversaries, graduations, and baby
showers. This frequent experience of gift-giving can
10 engender ambivalent feelings in gift-givers. Many
relish the opportunity to buy presents because
gift-giving offers a powerful means to build stronger
bonds with one’s closest peers. At the same time,
many dread the thought of buying gifts, they worry
15 that their purchases will disappoint rather than
delight the intended recipients.
Anthropologists describe gift-giving as a positive
social process, serving various political, religious, and
psychological functions. Economists, however, offer
20 a less favorable view. According to Waldfogel (1993),
gift-giving represents an objective waste of resources.
People buy gifts that recipients would not choose to
buy on their own, or at least not spend as much
money to purchase (a phenomenon referred to as
25 ‘‘the deadweight loss of Christmas”). To wit, givers
are likely to spend $100 to purchase a gift that
receivers would spend only $80 to buy themselves.
This ‘‘deadweight loss” suggests that gift-givers are
not very good at predicting what gifts others will
30 appreciate. That in itself is not surprising to social
psychologists. Research has found that people often
struggle to take account of others’ perspectives—
their insights are subject to egocentrism, social
projection, and multiple attribution errors.
35 What is surprising is that gift-givers have
considerable experience acting as both gift-givers and
gift-recipients, but nevertheless tend to overspend
each time they set out to purchase a meaningful gift.
In the present research, we propose a unique
40 psychological explanation for this overspending
problem—i.e., that gift-givers equate how much they
spend with how much recipients will appreciate the
gift (the more expensive the gift, the stronger a
gift-recipient’s feelings of appreciation). Although a
45 link between gift price and feelings of appreciation
might seem intuitive to gift-givers, such an
assumption may be unfounded. Indeed, we propose
that gift-recipients will be less inclined to base their
feelings of appreciation on the magnitude of a gift
50 than givers assume.
Why do gift-givers assume that gift price is closely
linked to gift-recipients’ feelings of appreciation?
Perhaps givers believe that bigger (i.e., more
expensive) gifts convey stronger signals of
55 thoughtfulness and consideration. According to
Camerer (1988) and others, gift-giving represents a
symbolic ritual, whereby gift-givers attempt to signal
their positive attitudes toward the intended recipient
and their willingness to invest resources in a future
60 relationship. In this sense, gift-givers may be
motivated to spend more money on a gift in order to
send a “stronger signal” to their intended recipient.
As for gift-recipients, they may not construe smaller
and larger gifts as representing smaller and larger
65 signals of thoughtfulness and consideration.
The notion of gift-givers and gift-recipients being
unable to account for the other party’s perspective
seems puzzling because people slip in and out of
these roles every day, and, in some cases, multiple
70 times in the course of the same day. Yet, despite the
extensive experience that people have as both givers
and receivers, they often struggle to transferinformation gained from one role (e.g., as a giver)
and apply it in another, complementary role (e.g., as
75 a receiver). In theoretical terms, people fail to utilize
information about their own preferences and
experiences in order to produce more efficient
outcomes in their exchange relations. In practical
terms, people spend hundreds of dollars each year on
gifts, but somehow never learn to calibrate their gift
expenditures according to personal insight.
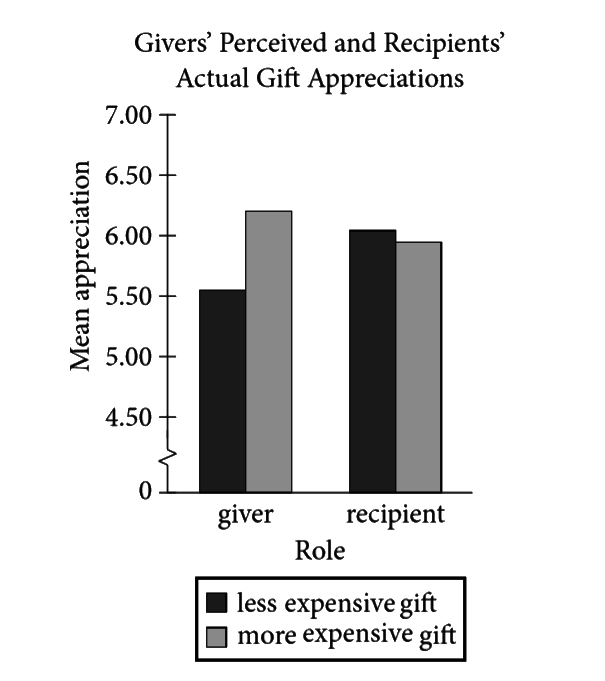
17. Which choice provides the best evidence for the answer to the previous question?ALines 53-55 (“Perhaps . . . consideration”)BLines 55-60 (“According . . . relationship”CLines 63-65 (“As . . . consideration”)DLines 75-78 (“In . . . relations”) 18

A jeweler makes beads for a bracelet by melting silver into spherical molds. Each mold has a diameter of 1 centimeters. After the silverhardents, the jeweler drills a small cylindrical hole through the center of the bead for the chain as shown. The drill bit has a diameter of 4 millimeters. If the jeweler strings a total of 15 beads on an elastic band, what is the approximate volume of silver, in cubic centimeters, on the bracelet? (Note: There are 10 millimeters in 1 centimeter.)
Note: The volume is approximate because the top and bottom of the cylindrical piece that is drilled out is slightly curved.
View SolutionAn isolated smooth ring of mass M = 2m with two small beads each of mass m is as shown in the figure. Initially both the beads are at diametrically opposite points and have velocity v0 (for each) in same direction. The speed of the beads just before they collide for the first time is (complete system is placed on a smooth horizontal surface and assume each point of ring is touching the surface)

View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

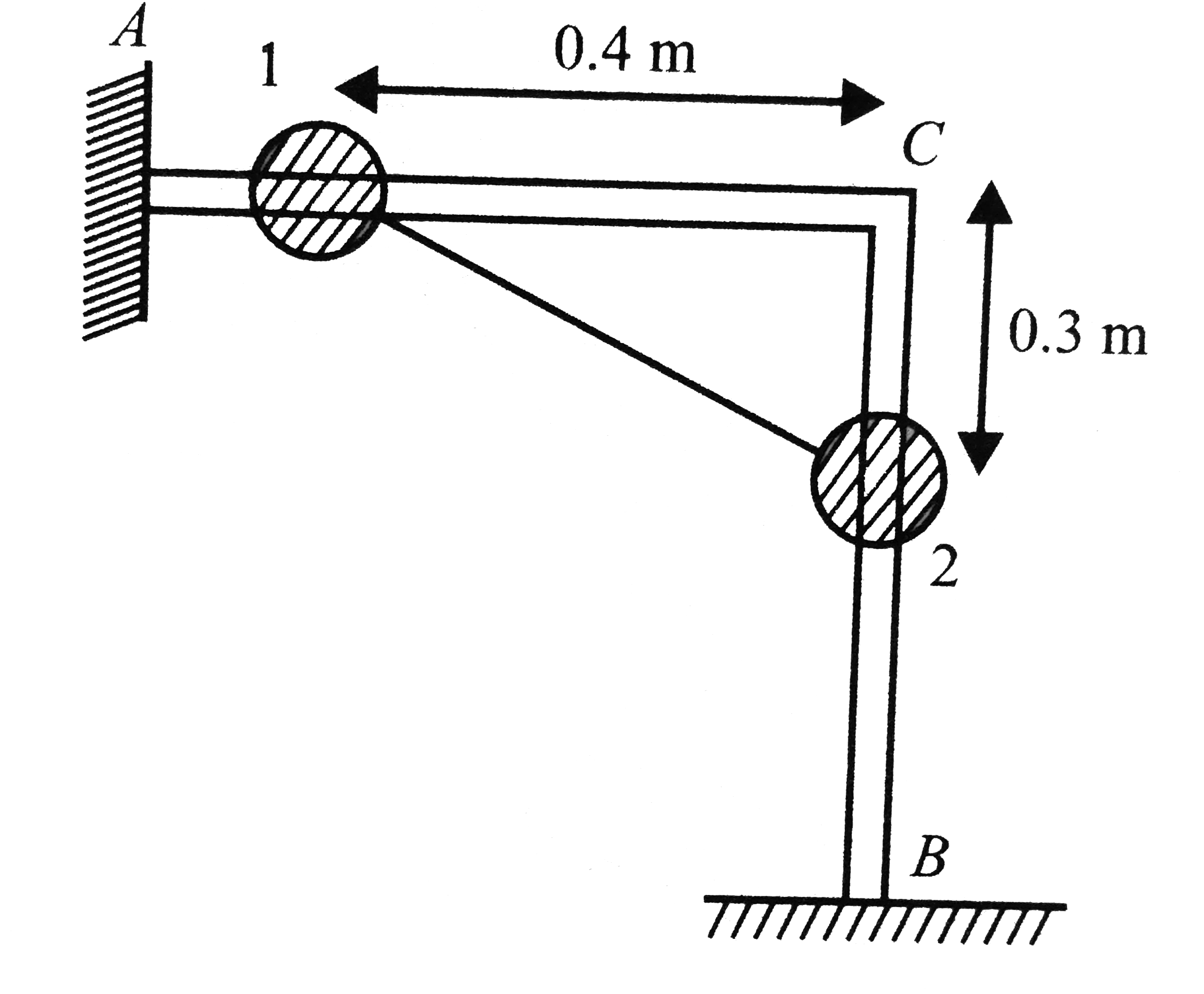
View SolutionTwo identical beads, each of m=100g, are connected by an inextensible massless string, which can slide along the two arms AC and BC of a rigid smooth wire frame in a vertical plane. If the system is released from rest, the kinetic energy of the first bead when the second bead has moved down by a distance of 0.1m is ×x10−3J. Find the value of x(g=10ms−2) (shown situation is after movement of 0.1m).
View SolutionA small, electrically charged bead can slide on a circular, frictioless, insulating rod. A point - like electric dipole (→P) is fixed at the centre of the circle with the dipole.s axis lying in the plane of the circle. Intially the bead is on the plane of symmetry of the dipole, as shown in the figure. The bead is slightly displaced along ring, tangentially with intial speed very close to zero. (Ignore the effect of gravity, assuming that the electric forces are much greater than the gravitational ones).
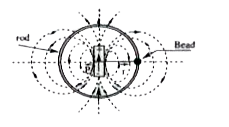
The normal force exerted by rod on the bead is (q = angle between an radius vector of bead, (considering dipole as origin)
View Solution
