The tables above represent data points for two linear equations. If the two equations form a system, what is the x-coordinate of the solution to that system ?
4
6
8
-4
The correct Answer is:C
In the table for Equation 1, the x-values increase by 2 each time and the y-values decrease by 2. In the table for Equation 2, the x-values increase by 4 each time and the y-values increase by 1. Use these patterns to continue the tables.
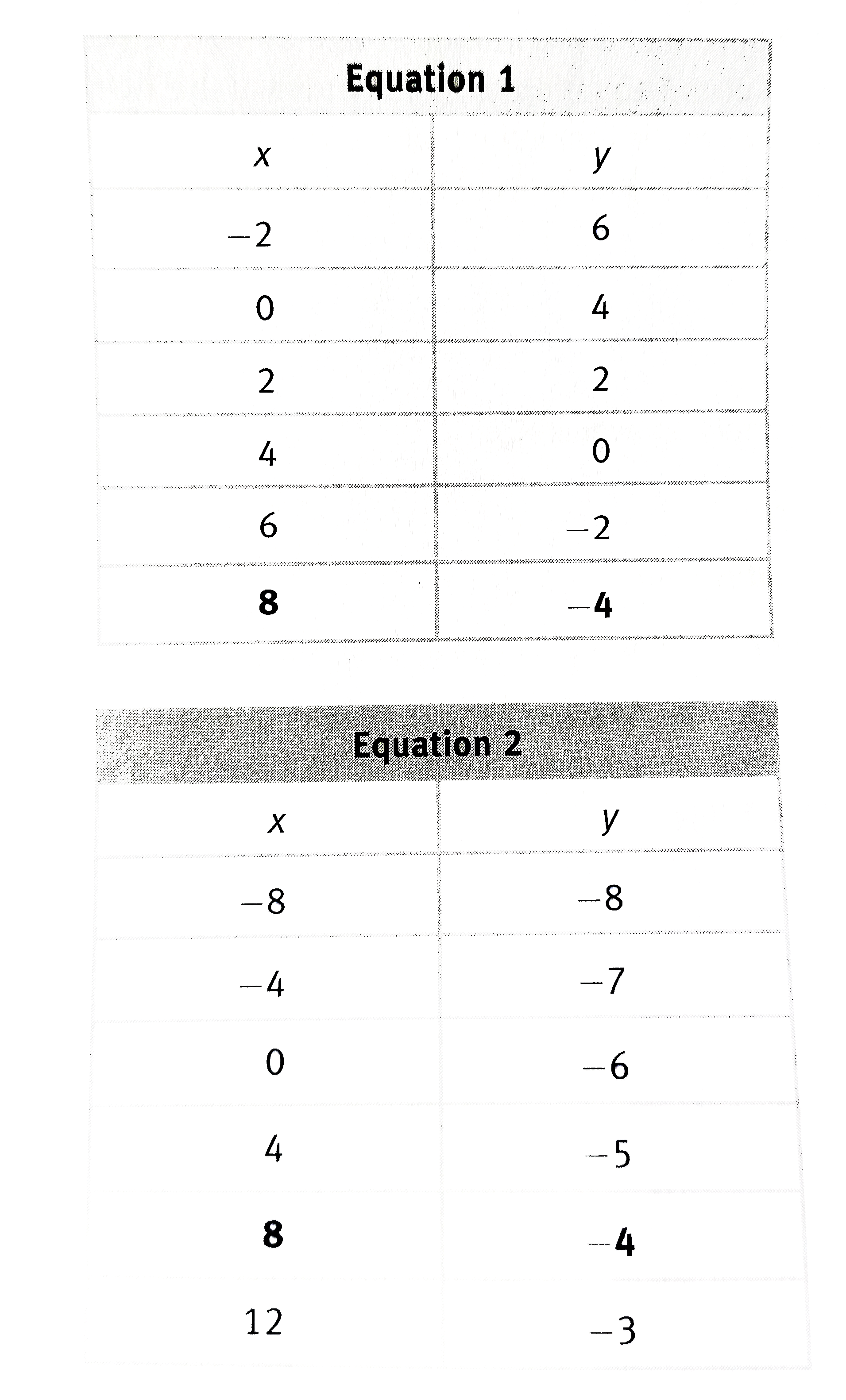
The point (8,−4) satisfies both equations, so the x-cordinate of the solution to the system is 8.
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - SYSTEMS OF LINEAR EQUATIONSEXERCISE - SUBSTITUTION1videos
SYSTEMS OF LINEAR EQUATIONS
- BOOK - KAPLANCHAPTER - SYSTEMS OF LINEAR EQUATIONSEXERCISE - COMBINATION1videos
SYSTEMS OF LINEAR EQUATIONS
- BOOK - KAPLANCHAPTER - SYSTEMS OF LINEAR EQUATIONSEXERCISE - ON TEST DAY1videos
SYSTEMS OF LINEAR EQUATIONS
- BOOK - KAPLANCHAPTER - SCATTERPLOTSEXERCISE - SCATTERPLOT MODELING1videos
SCATTERPLOTS
- BOOK - KAPLANCHAPTER - THE MATHOD OF SAT MATH QUESTIONS EXERCISE - TRY ON YOUR OWN10videos
THE MATHOD OF SAT MATH QUESTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
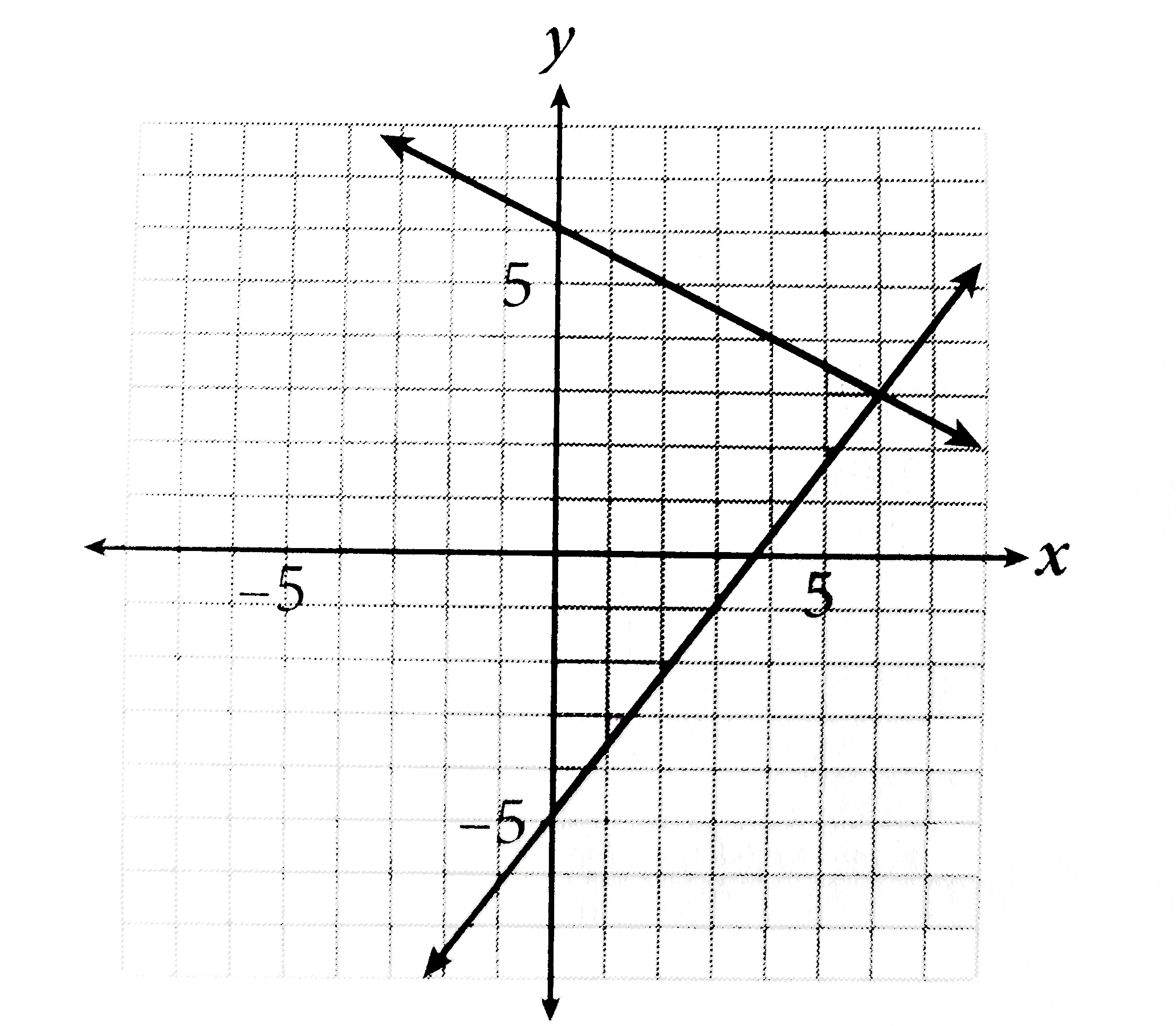
What is tha y-coordinate of the solution to the system shown above ?A−5B3C5D6 - Question 2 - Select One

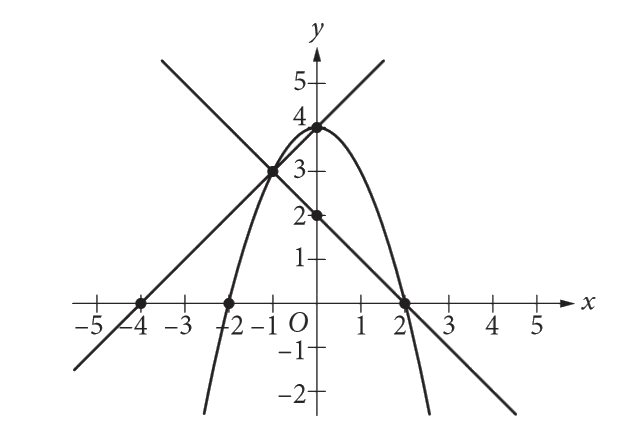
The lines graphed in the xy-plane above represent a system of two linear equations. What is the solution (x,y) to the system?A(-1,-6)B(0,-3)C(2,3)D(3,0) - Question 3 - Select One
If the system of linear equations above has o solution, and a is a constant, then what is the value of a ?
A−2B−12C2D6
If (x,y) is a solution to the system of equations above, what is the value of x2 ?
View SolutionBen correctly solves a system of two linear equations and finds that the system has an infinite number of solutions. If one of the two equations is 3(x+y)=6−x, which could be the other equation in this system?
View SolutionThe x-coordinates of the solutions to a system of equations are 3.5and6. Which of the following could be the system ?
View Solution
A system of three equations is shown graphically in the xy-plane above. How many solutions does the system have ?View Solution(x−2)2+y2=36
y=−x+2
The equation above represent a circle and a line that intersects the circle across its diameter . What is the point of intersection of the two equations that lies in Quadrant II?View Solution