A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are
A. y=2√3+x+1,y=−2√3x−1
B. y=1√3x,y=0
C. y=√32x+1,y=−√32x−1
D. y=√3x,y=0
(x−2√3)2+(y−1)2=1
(x−2√3)2+(y+12)2=1
(x−√3)2+(y+1)2=1
(x−√3)2+(y−1)2=1
The correct Answer is:4
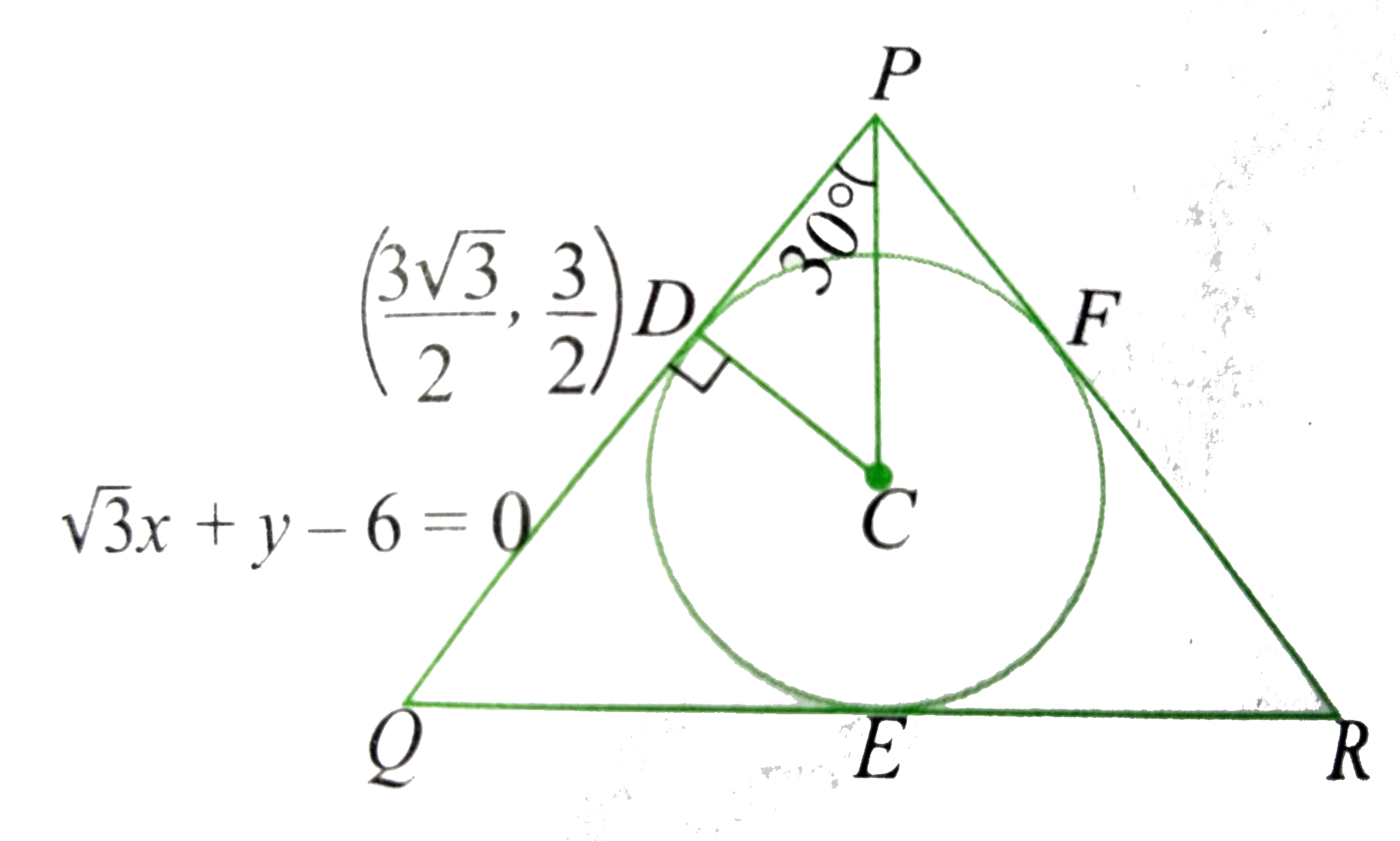
Equation of PQ is L1:√3x+y−6=0 (1)
Slope of PQ is −√3
∴Slope of CD is 1√3.
∴Equation of line CD in parametric from is
x−3√32cos30∘=y−32sin30∘=r
or x−3√32√32=y−3212=r
For centre C, r=±1
Two possible coordinates of centre are (2√3,2),(√3,1)
According to the question, center lies on the same side where origin lies with respect to line PQ.
Now L1(0,0)=−6<0
And L1(√3,1)=3+1−6<0
So Centre C must be (√3,1)
Hence, equation of the circle is (x−√3)2+(y−1)2=1
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
A circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
The equation of circle C is
View SolutionA circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
Equations of the sides QR, RP are
View Solution
Knowledge Check
A circle of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QH and RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3√32,32). Further, it is given that the origin and the centre of C are on the same side of the line PQ.
Points E andF are given byA(√32,32),(√3,0)B(√32,12),(√3,0)C(√32,32),(√32,12)D(32,√32),(√32,12)PQRS is a quadrilateral having 3 4 5 6 points on PQ , QR, RS and SP respectively. The number of triangles with vertices on different sides is
A220B270C282Dnone of these
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Equation of the sides QR,RP are : (A) y=2√3x+1,y=2√3x−1 (B) y=1√3x,y=0 (C) y=√32x+1,y=√32x−1 (D) y=√3x,y=0
View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Point E and F are given by : (A) (√32,32),(√3,0) (B) (√32,32),(√32,12) (C) (32,√32),(√32,12)
View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (3√32,32) The equation of circle C is : (A) (x−2√3)2+(y−1)2=1 (B) (x−2√3)2+(y+12)2=1 (C) (x−√3)2+(y+1)2=1 (D)(x−√3)2+(y−1)2=1
View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32) The equation of circle C is : (A) (x−2√3)2+(y−1)2=1 (B) (x−2√3)2+(y+12)2=1 (C) (x−√3)2+(y+1)2=1 (D)(x−√3)2+(y−1)2=1
View SolutionNumber of equilateral triangle with y=√3(x−1)+2;y=−√3x as two of its sides is
View SolutionThe vertex P of an equilateral triangle △PQR is at (2,3) and the equation of the opposite side QR is given by x+y=2. Find the possible equations of the side PQ.
View Solution
