A circle C whose radius is 1 unit touches the x-axis at point A. The center Q of C lies in the first quadrant. The tangent from the origin O to the circle touches it at T and a point P lies on its such that ΔOAP is a right - angles triangle at A and its perimeter is 8 units.
The length of PQ is Solution in Bengali
3y=4x
x−√2y=0
y−√3x=0
none of these
The correct Answer is:1
AP=AQ+PQ=1+5/3=8/3
So, slope of OP is 4/3
Hence, equation of OP is 4x−3y=0.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE7videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE21videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)3videos
CIRCLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Match the following lists.
 04:15View Solution
04:15View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2+gx+fy+7=0 , then the value of |f+g| is__________
07:16View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
02:15View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is02:44View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is02:36View SolutionA circle touches the hypotenuse of a right angled triangle at its midle point and passes through the middle point of shorter side.If 3 unit and 4 unit be the length of the sides and 'r be the radius of the circle,then find the value of 3r
08:03View SolutionA circle C whose radius is 1 unit,touches the x-axis at point A.The centre Q of C lies in first quadrant.The tangent from origin O to the circie touches it at T and a point P lies on it such that Delta OAP is a right angled triangle at A and its perimeter is 8units.The length of QP is
View Solutionकिसी वृत्त का केंद्र O हैं| बाहरी बिंदु P से वृत्त पर एक स्पर्श रेखा PQ हैं, जो वृत्त को Q बिंदु पर स्पर्श करती हैं, तो ∠PQO= |
View SolutionIn the figure, sides of △ABC are tangents to the circle touching the circle at points P, Q abd R as shown. If AQ=3 cm, BR=7 cm and PC= 4 c m, then perimeter of △ABC is
 02:55View Solution
02:55View SolutionABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
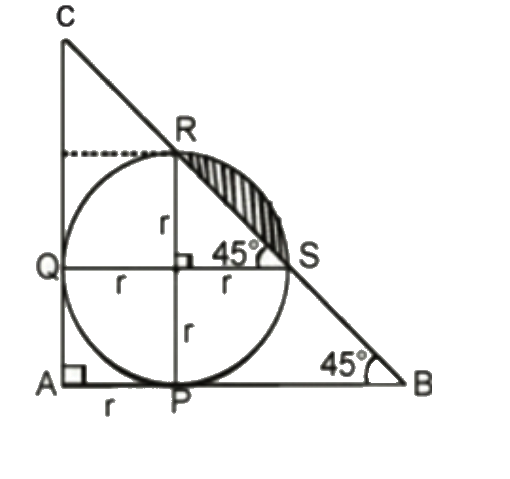 04:36View Solution
04:36View SolutionA circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that ΔOAP is a right angled triangle at A and its perimeter is 8 units.
Equation of tangent OT is03:52View SolutionA circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that ΔOAP is a right angled triangle at A and its perimeter is 8 units.
If tangent OT cuts the two parallel tangents (one of them is OA) at O and R, then equation of circle circumscribing the ΔORQ is03:16View SolutionA circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that ΔOAP is a right angled triangle at A and its perimeter is 8 units.
Equation of the larger circle which touches the tangents drawn from origin to the circle C and the circle C extermally is06:06View SolutionA circle of radius 5 units touches both the axes and lies in the first quadrant. If the circle makes one complete roll on x-axis along the positive direction of x-axis, then its equation in new position is:
01:51View Solution5 సెంమీ, వ్యాసార్థముగా గల వృత్తాన్ని PQ స్పర్శరేఖ p వద్ద తాకింది. వృత్త కేంద్రము 'O' నుండి స్పర్శరేఖ పై గల బిందువు Q నకు దూరము OQ=13 సెంమీ, అయిన PQ పొడవును కనుగొనుము.
02:39View SolutionO' కేంద్రముగా గల వృత్తానికి, బాహ్య బిందువు P నుండి గీసిన స్పర్శరేఖ PQ, వృత్తాన్ని Q వద్ద తాకుచున్నది. వృత్త వ్యాసార్థం 9 సెంమీ మరియు PQ=12 సెంమీ అయిన వృత్త కేంద్రం నుండి P ఎంత దూరంలో ఉన్నది?
01:36View Solution

