A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units. The length of $Q P$ is

$1 / 2$

$4 / 3$

$5 / 3$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

Given $Q T = Q A = 1$ .

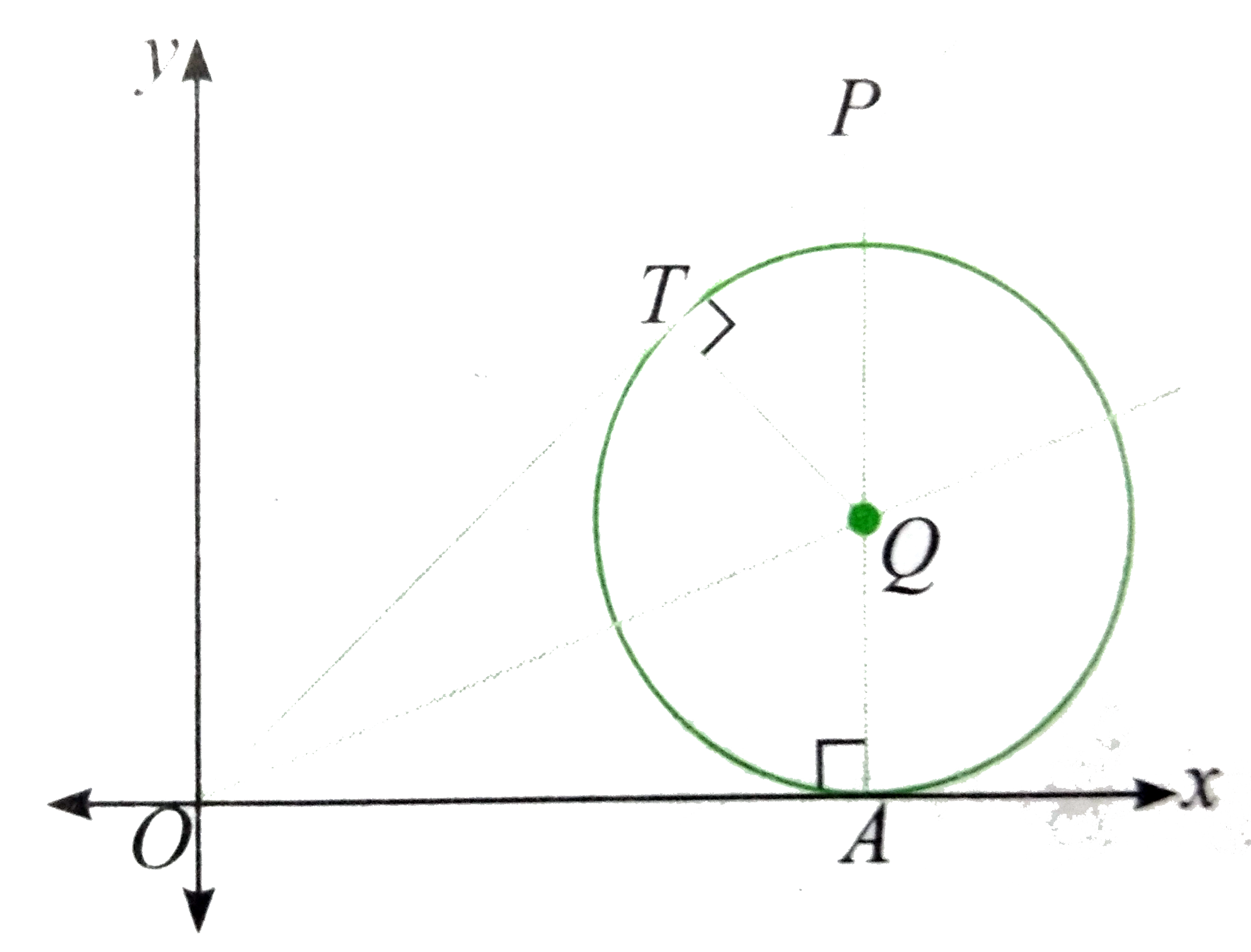
Let $P Q = x$ . Then $P T = \sqrt{x^{2} - 1}$ .
$Δ T Q P$ and $Δ A O P$ are similar triangles. Then ,
$\frac{O A}{T Q} = \frac{A P}{T P}$
$\Rightarrow O T = O A = \frac{x + 1}{\sqrt{x^{2} - 1}}$
Perimeter of $Δ O A P$ is 8 units.
$∴ 1 + x + \frac{2 (x + 1)}{\sqrt{x^{2} - 1}} = 8$ or $x = \frac{5}{3}$

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units.
Equation of tangent OT is
A $x - \sqrt{3} y = 0$
B $x - \sqrt{2} y = 0$
C $y - \sqrt{3} x = 0$
Dnone of these
Question 2 - Select One
A circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units.
Equation of the larger circle which touches the tangents drawn from origin to the circle C and the circle C extermally is
A ${x - 2 (2 - \sqrt{3})}^{2} + {(y - 2)}^{2} = 4$
B ${x - 2 (2 + \sqrt{3})}^{2} + {y - 2 (7 + 2 \sqrt{3})}^{2} = 4 {(7 + 2 \sqrt{3})}^{2}$
C ${x - 3 (2 - \sqrt{3})}^{2} + {(y - 3)}^{2} = 9$
Dnone of these
Question 3 - Select One
A circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units.
If tangent OT cuts the two parallel tangents (one of them is OA) at O and R, then equation of circle circumscribing the $Δ O R Q$ is
A $x^{2} + y^{2} - \sqrt{3} x - y = 0$
B $x^{2} + y^{2} - \sqrt{3} x - 2 y = 0$
C $x^{2} + y^{2} - 2 \sqrt{3} x - 2 y = 0$
Dnone of these

CENGAGE-CIRCLE -Exercise (Comprehension)

Home
Ask Doubt
Profile

A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that ΔOAP is a right angled triangle at A and its perimeter is 8 units. The length of QP is

The correct Answer is:3

Given QT=QA=1. Let PQ=x. Then PT=√x2−1. ΔTQP and ΔAOP are similar triangles. Then , OATQ=APTP ⇒OT=OA=x+1√x2−1 Perimeter of ΔOAP is 8 units. ∴1+x+2(x+1)√x2−1=8 or x=53

Topper's Solved these Questions

Similar Questions

Knowledge Check

A circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that ΔOAP is a right angled triangle at A and its perimeter is 8 units. Equation of tangent OT is

CENGAGE-CIRCLE -Exercise (Comprehension)

A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units. The length of $Q P$ is

A circle C whose radius is 1 unit, thuches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circle touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units.
Equation of tangent OT is