Doubtnut Promotions Sticky

A circle C1 of radius b touches the circle x2+y2=a2 externally and has its centre on the positiveX-axis; another circle C2 of radius c touches the circle C1, externally and has its centre on the positive x-axis. Given a<b<c then three circles have a common tangent if a,b,c are in

A

AP

B

GP

C

HP

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:2

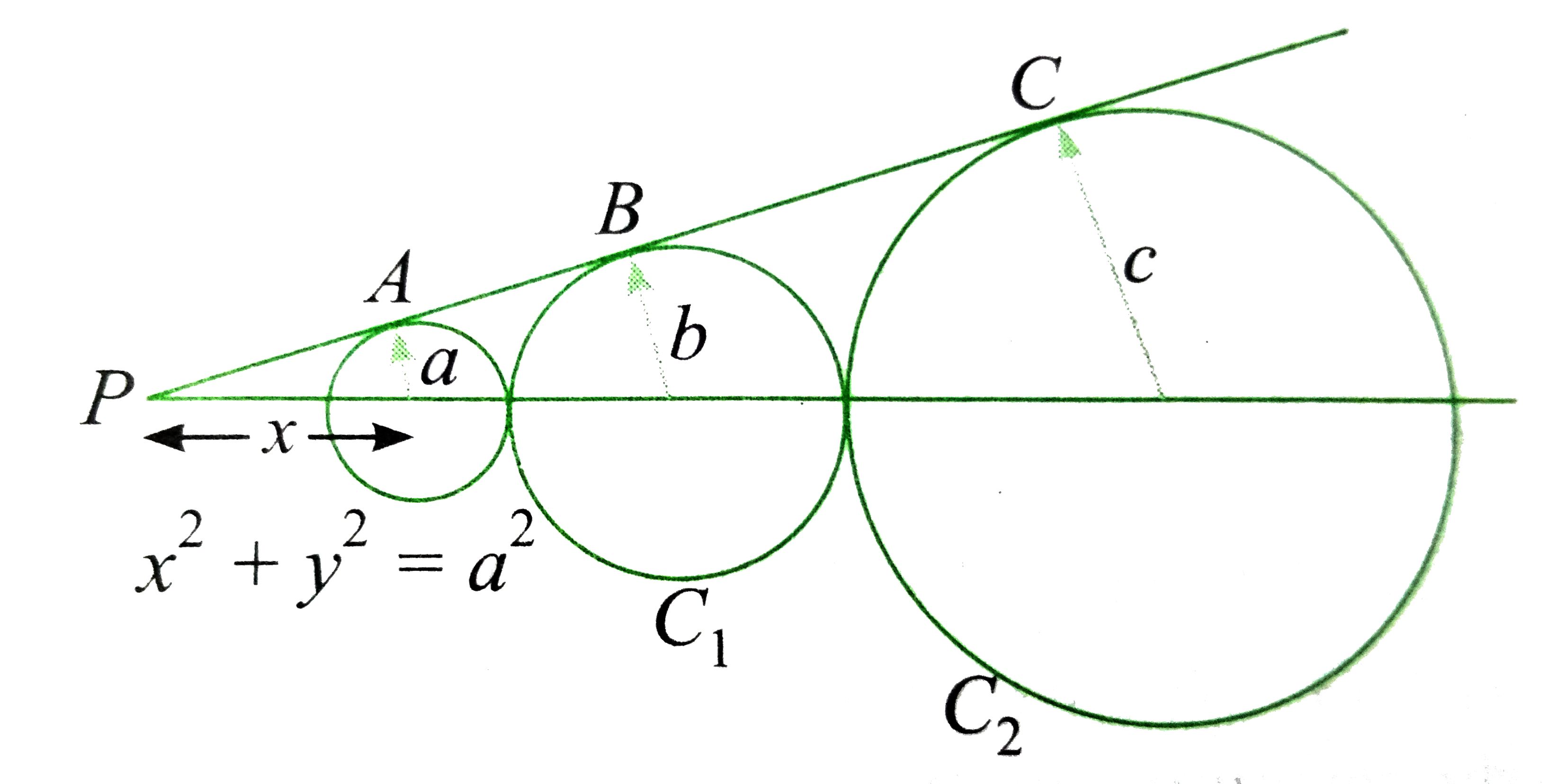
ocr_image
From the figure,
ax=bx+a+b=cxa+2b+c
∴ax+a2+ab=bx (Comparing first two )
or x=a2+abb−a
ax+a2+2ab+ac=cx (Comparing first and third )
∴a2+abb−a=a2+2ab+acc−a a2c−a3+abc−a2b=a2b+2ab2+abc−a3−2a2b−a2c
or ac=b2
Therefore, a,b, and c are in GP.

|
Updated on:21/07/2023
Class 12MATHSCIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    A circle C touches the x-axis and the circle x2+(y−1)2=1 externally, then locus of the centre of the circle C is given by

    A{(x,y):x2=4y}∪{(0,y):y≤0}.
    B{(x,y):y=x2}∪{(0,y):y≤0}
    C{(x,y):x2+(y−1)2=0}∪{(0,y):y≤0}
    D{(x,y):x2+4y=0}∪{(0,y):y≤0}
  • Question 2 - Select One

    The locus of centre of the circle which touches the circle x2+(y−1)2=1 externally and also touches x-axis is

    A{(x,y):x2+(y−1)2=4}∪{(x,y):y<0}
    B{(x,y):x2=4y}∪{(0,y):y<0}
    C{(x,y):x2=y}∪{(0,y):y<0}
    D{(x,y):x2=4y}∪{(x,y):y>0}
  • Question 3 - Select One

    The locus of centre of the circle which touches the circle x2+(y−1)2=1 externally and also touches x-axis is

    A{(x,y):x2+(y−1)2=4}∪{(x,y):y>0}
    B{(x,y):x2=4y}∪{(0,y):(y<0)}
    C{(x,y):x2=y}∪{(0,y):y<0}
    D{(x,y):x2=4y}∪{(x,y):y<0}