A circle touches the parabola $y^{2} = 4 x$ at $(1, 2)$ and also touches its directrix. The y-coordinates of the point of contact of the circle and the directrix is-

A

$\sqrt{2}$

B

$2$

C

$2 \sqrt{2}$

D

$4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

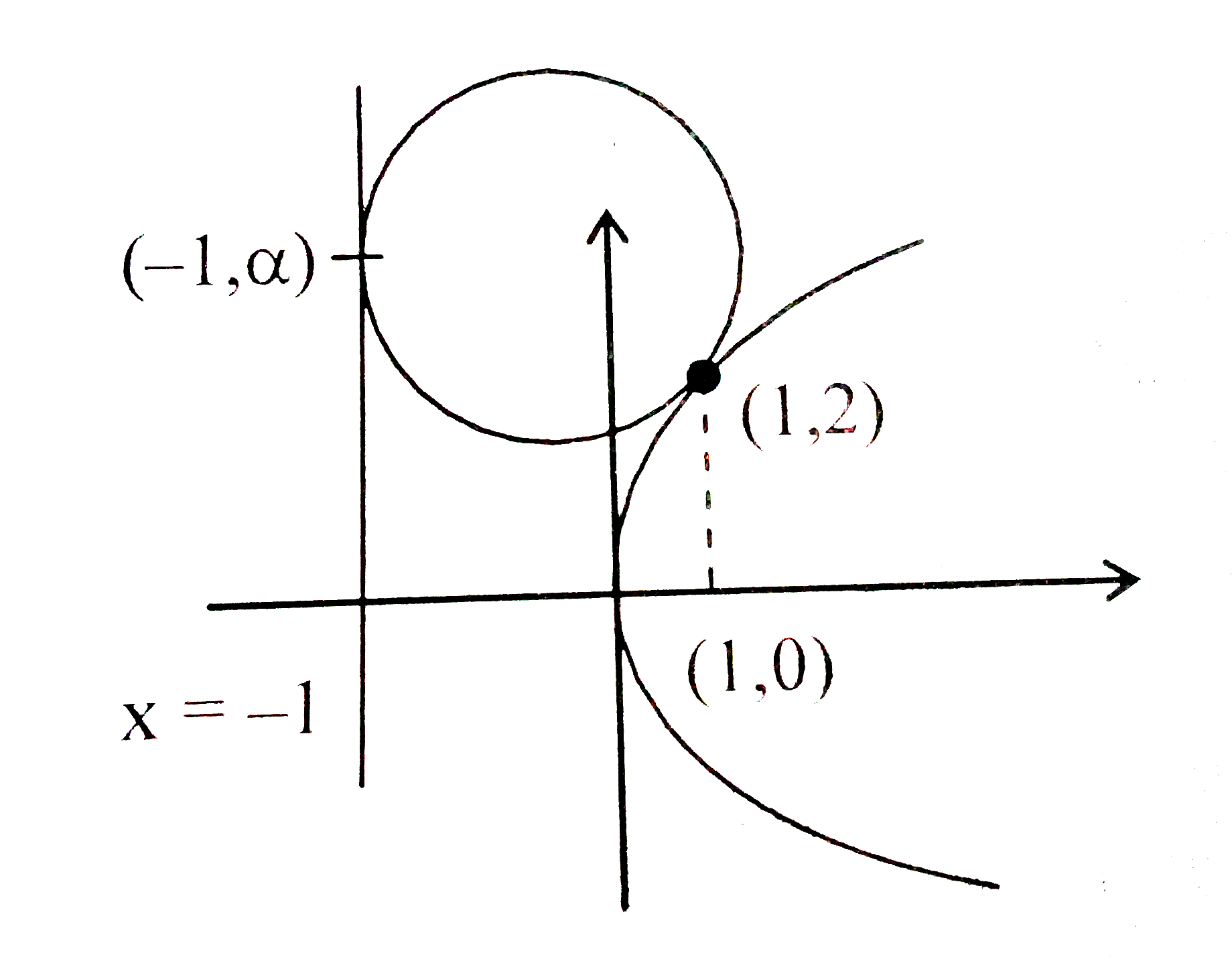
$y^{2} = 4 x$
$2 y \frac{d y}{d x} = 4$
$m_{T} = \frac{2}{y} = \frac{2}{2} = 1$
Circle $\to S + λ L = 0$
${(x + 1)}^{2} + {(y - α)}^{2} + λ (x + 1) = 0 \dots.. (1)$
differentiate
$2 {(x + 1)}^{2} + 2 (y - α) \frac{d y}{d x} + λ = 0$
$x = 1, y = 2$
$4 + 2 (2 - α) m_{T} + λ = 0$
$λ = 2 α - 8 ...... (2)$
$(1, 2)$ satisfies eq. (1)
$2^{2} + {(2 - α)}^{2} + 2 λ = 0$
$α^{2} - 4 α + 8 + 2 (2 α - 8) = 0$
$α^{2} = 8$
$α = 2 \sqrt{2}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

KVPY PREVIOUS YEAR-KVPY-exercise

Home
Ask Doubt
Profile