A circle touches two of the smaller sides of a ΔABC(a<b<c) and has its centre on the greater side. Then, find the radius of the circle.
To solve the problem of finding the radius of a circle that touches two sides of triangle ΔABC with a<b<c and has its center on the greater side, we can follow these steps:
1. Identify the Triangle and Circle Configuration:
- We have triangle ABC where a,b,c are the lengths of the sides opposite to vertices A,B,C respectively, with a<b<c.
- The circle touches sides BC and AC and its center O lies on side AB.
2. Understanding the Tangents:
- Since the circle touches sides BC and AC, we can denote the points of tangency as P (on BC) and Q (on AC).
- The radius R of the circle is perpendicular to the tangents at points P and Q.
3. Area of Triangle ABC:
- The area Δ of triangle ABC can be calculated using Heron's formula:
s=a+b+c2(semi-perimeter)
Δ=√s(s−a)(s−b)(s−c)
4. Area of Triangles OBC and OAC:
- The area of triangle OBC can be expressed as:
AreaOBC=12×BC×R=12×a×R
- The area of triangle OAC can be expressed as:
AreaOAC=12×AC×R=12×b×R
5. Total Area Relation:
- The total area of triangle ABC is the sum of the areas of triangles OBC and OAC:
Δ=AreaOBC+AreaOAC
Δ=12aR+12bR=R2(a+b)
6. Setting Up the Equation:
- From the area expressions, we have:
Δ=R2(a+b)
- Rearranging gives:
R=2Δa+b
7. Final Result:
- Therefore, the radius R of the circle is:
R=2Δa+b
- We have triangle ABC where a,b,c are the lengths of the sides opposite to vertices A,B,C respectively, with a<b<c.
- The circle touches sides BC and AC and its center O lies on side AB.
- Since the circle touches sides BC and AC, we can denote the points of tangency as P (on BC) and Q (on AC).
- The radius R of the circle is perpendicular to the tangents at points P and Q.
- The area Δ of triangle ABC can be calculated using Heron's formula:
s=a+b+c2(semi-perimeter)
Δ=√s(s−a)(s−b)(s−c)
- The area of triangle OBC can be expressed as:
AreaOBC=12×BC×R=12×a×R
- The area of triangle OAC can be expressed as:
AreaOAC=12×AC×R=12×b×R
- The total area of triangle ABC is the sum of the areas of triangles OBC and OAC:
Δ=AreaOBC+AreaOAC
Δ=12aR+12bR=R2(a+b)
- From the area expressions, we have:
Δ=R2(a+b)
- Rearranging gives:
R=2Δa+b
- Therefore, the radius R of the circle is:
R=2Δa+b
Similar Questions
Knowledge Check
Three circles touch each other externally. A triangle is formed when the centres of these circles are joined together. Find the radii of the circles, if the sides of the triangle formed are 6 cm, 8 cm and 9 cm.
A4.2cm,2.5cm and 5.8 cmB4.5cm,2.5cm and 7.5 cmC3.5cm,2.5cm and 5.5 cmD3.5cm,12.5cm and 7.5 cm
A circle touches the hypotenuse of a right angled triangle at its middle point and passes through the mid-point of the shorter side. If aandb(a<b) be the lengths of the sides, then prove that the radius of the circle is b4a√a2+b2
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View Solutionin the adjoining figure ABCD is a square of side 14 cm. Find the radius of the circle
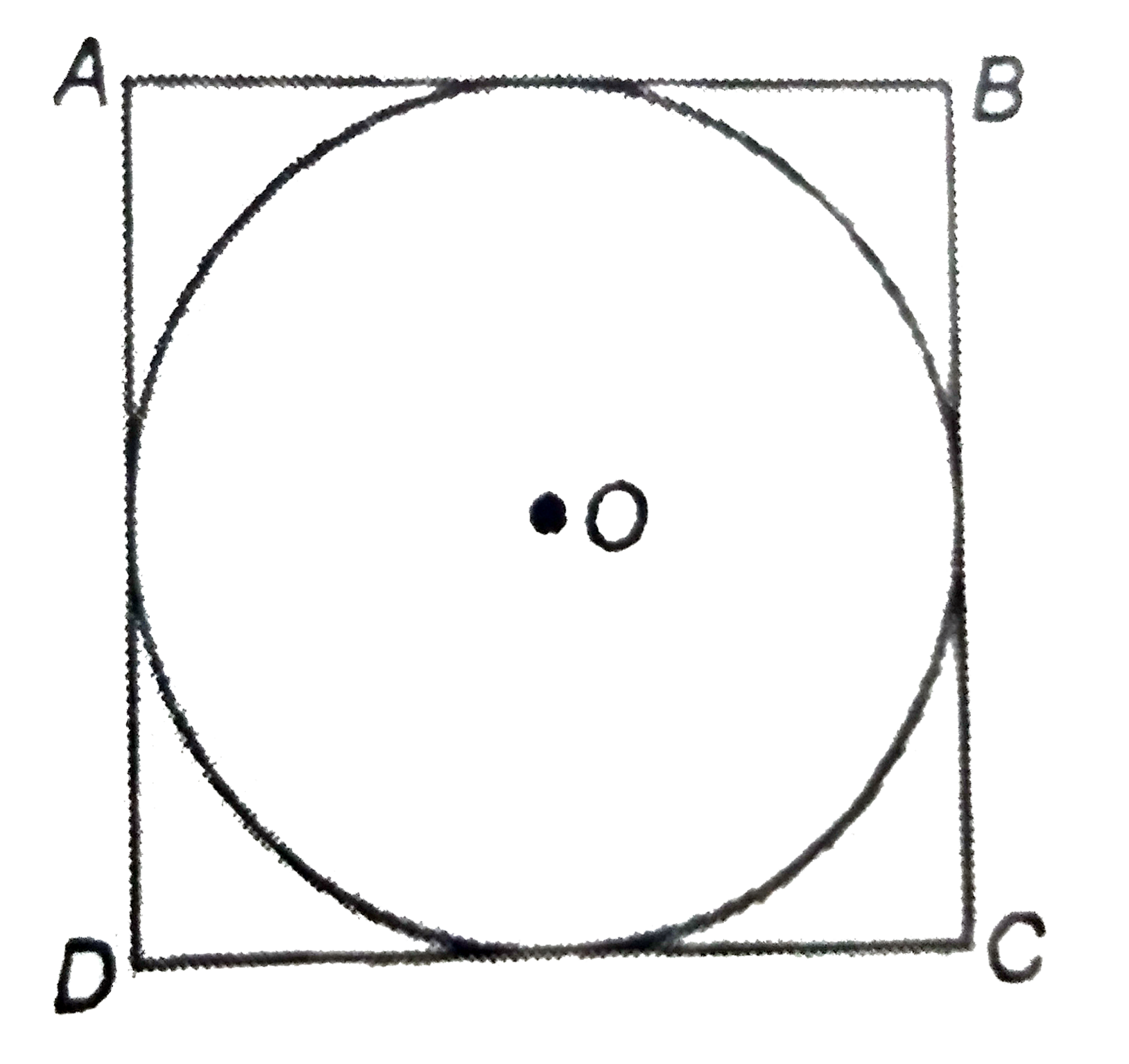
View SolutionABCD is a square of side length 2 units. C1 is the circle touching all the sides of the square ABCD and C2 is the circumcircle of square ABCD. L is a fixed line in the same plane and R is fixed point. If a circle is such that it touches the line L and the circle C1 externally, such that both the circles are on the same side of the line, then the locus of centre of the circle is
View SolutionChords AB and CD of a circle are parallel to each other and lie on opposite sides of the centre of the circle. If AB = 36 cm, CD = 48 cm and the distance between the chords is 42 cm, find the radius of the circle.
View SolutionA circle C1 of radius b touches the circle x2+y2=a2 externally and has its centre on the positiveX-axis; another circle C2 of radius c touches the circle C1, externally and has its centre on the positive x-axis. Given a<b<c then three circles have a common tangent if a,b,c are in
View SolutionA circle touches the line L and the circle C1 externally such that both the circles are on the same side of the line, then the locus of centre of the circle is :
View Solution
