A circle with center at the origin and radius equal to a meets the axis of x at AandB.P(α) and Q(β) are two points on the circle so that α−β=2γ , where γ is a constant. Find the locus of the point of intersection of AP and BQ.Solution in Bengali
Let
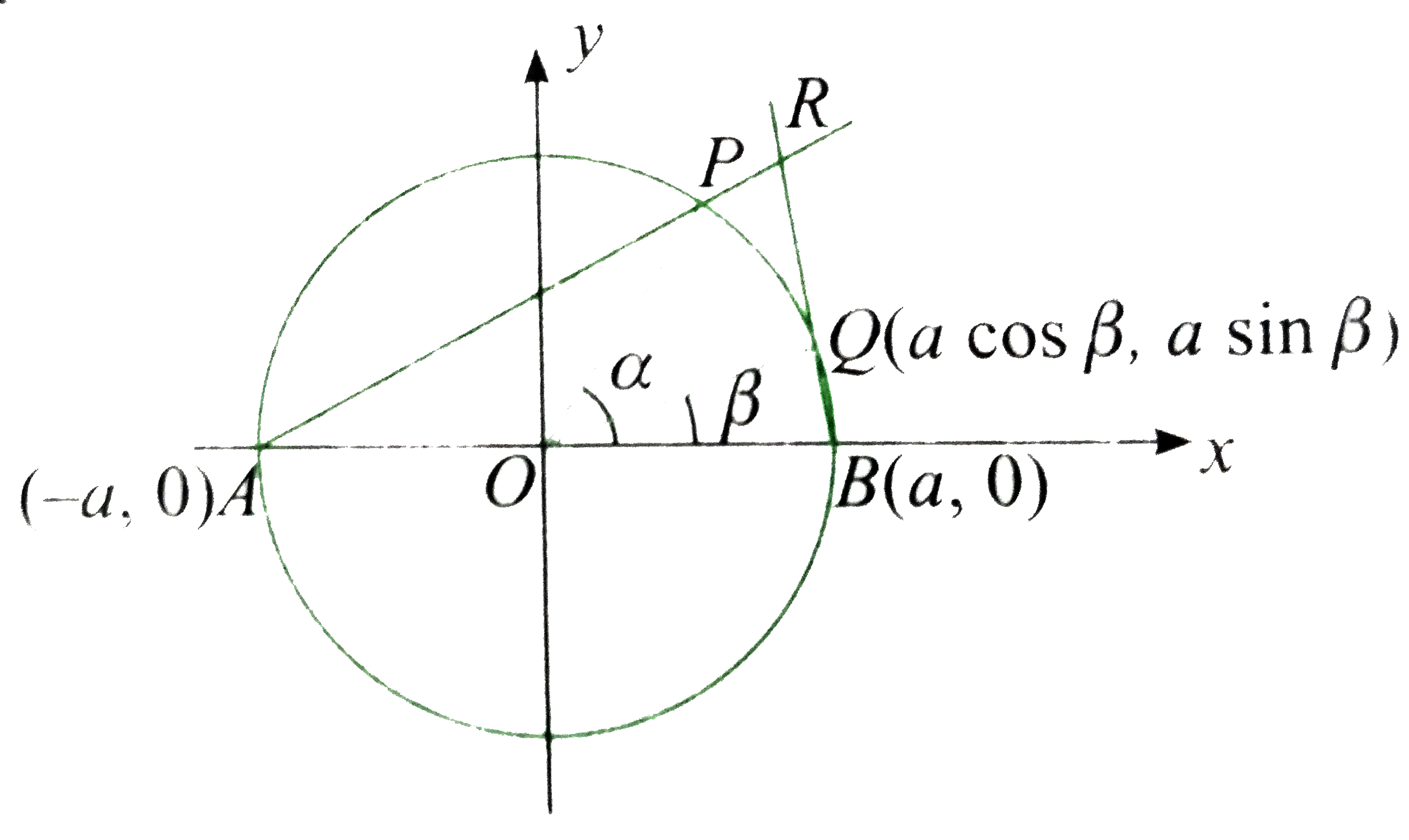
The coordinates of A are ( -a,0) and that of P are (acosα,asinα).
Therefore, the equation of AP is
y=asinαa(cosα+1)(x+a)
or y=tan.α2(x+a) (1)
Similarly, the equationof BQ is
y=asinβa(cosβ−1)(x−a)
or y=−cot.β2(x−a) (2)
We now eliminate α and β from (1) and (2). Therefore,
tan.α2=ya+x,tan.β2=a−xy
Now, α−β=2γ⇒γ=α2−β2
∴tanγ=tan.α2−tan.β21+tan.α2tan.β2=ya+x−a−xy1+ya+x.a−xy
or tanγ=y2−(a2−x2)(a+x)y+(a−x)y
=x2+y2−a22ay
or x2+y2−2aytanγ=a2
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionS is a circle having the center at (0,a) and radius b(b<a). A variable circle centered at (α,0) and touching the circle S meets the X-axis at MandN . Find the a point P on the Y-axis, such that ∠MPN is a constant for any choice of α
View SolutionA circle with center at the origin and radius equal to a meets the axis of x at AandB.P(α) and Q(β) are two points on the circle so that α−β=2y , where γ is a constant. Find the locus of the point of intersection of AP and BQ.
View SolutionIf α−β= constant, then the locus of the point of intersection of tangents at P(acosα,bsinα) and Q(acosβ,bsinβ) to the ellipse x2a2+y2b2=1 is: (a) a circle (b) a straight line (c) an ellipse (d) a parabola
View SolutionPoint of intersection of tangents at points P(α) and Q(β)
View SolutionIf α,β,γ be the zeros of the polynomial p(x) such that (α+β+γ)=3,(αβ+βγ+γα)=−10andαβγ=−24 then p(x) = ?
View SolutionA circle x2+y2=a2 meets the x-axis at A(-a,0) and B(a,0). P(α) and Q(β) are two points on the circle so that α−β=2γ, where γ is a constant. Find the locus of the point of intersection of AP and BQ.
View SolutionIf α,βandγ are the roots of the equation x3+px+q=0 (with p≠0andp≠0andq≠0), the value of the determinant
∣∣ ∣ ∣∣αβγβγαγαβ∣∣ ∣ ∣∣, is
View SolutionA plane cutting the axes in P, Q, R passes through (α−β,β−γ,γ−α). If O is the origin, then locus of centre of sphere OPQR is
View SolutionLet P(α,β,γ)andQ(1,−1,0) be points such that the mid-point of PQ is R(x,y,z). If x is the AM of αandβ,y is the G.M. of βandγandz is the H.M . Of γandα then :
View SolutionIf the eccentric angles of two points P and Q on the ellipse x2a2+y2b2 are α,β such that α+β=π2, then the locus of the point of intersection of the normals at P and Q is
View SolutionS is a circle having the center at (0,a) and radius b(b<a). A variable circle centered at (α,0) and touching the circle S meets the X-axis at MandN . Find the a point P on the Y-axis, such that ∠MPN is a constant for any choice of α
View SolutionA circle with center at the origin and radius equal to a meets the axis of x at AandB.P(α) and Q(β) are two points on the circle so that α−β=2γ , where γ is a constant. Find the locus of the point of intersection of AP and BQ.
View Solution
