A circular disk of unit radius is filled with a number of smaller circular disks arranged in the form of hexagon. Let $A_{n}$ denotes a stack of disks arranged in the shape of a hexagon having 'n' disks on a side. The figure shows the configuration $A_{3}$ . If A be the area of large disk, $S_{n}$ be the number of disks in $A_{n}$ configuration and $r_{n}$ be the radius of each disk in $A_{n}$ configuration, then $lim n \to \infty \frac{S_{n}}{n^{2}}$ $lim n \to \infty n r_{n}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for A circular disk of unit radius is filled with a number of smaller circular disks arranged in the form of hexagon. Let A_n denotes a stack of disks arranged in the shape of a hexagon having 'n' disks on a side. The figure shows the configuration A_3. If A be the area of large disk, S_n be the number of disks in A_n configuration and r_n be the radius of each disk in A_n configuration, then lim_(n->oo)(S_n)/n^2 lim_(n->oo) nr_n by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
The disks stores information in
ATables
BRows and columns
CBlocks
DTracks and sectors
Question 2 - Select One
A circular disk of radius 0.010 m rotates with a constant angular speed of 5.0 rev/s. What is the acceleration of a point on the edge of the disk?
A $0.31 m / s^{2}$
B $9.9 m / s^{2}$
Czero $m / s^{2}$
D $1.6 m / s^{2}$
Question 3 - Select One
A circular hole of radius $r$ is made in a disk of radius $R$ and of uniform thickness at a distance $a$ from the centre of the disk. The distance of the new centre of mass from the original centre of mass is

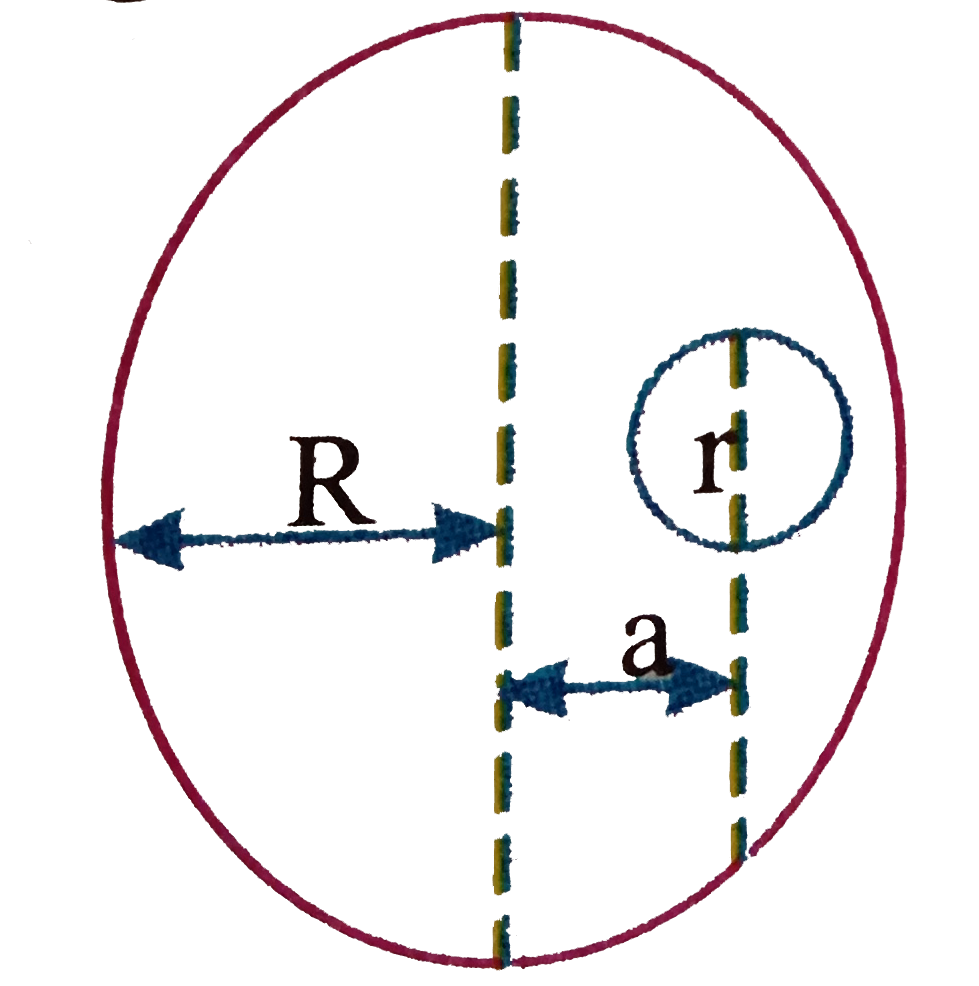A $\frac{a R^{2}}{R^{2} - r^{2}}$
B $\frac{a r^{2}}{R^{2} - r^{2}}$
C $\frac{a (R^{2} - r^{2})}{r^{2}}$
D $\frac{a (R^{2} - r^{2})}{R^{2}}$