Question

A company makes 3 model of calculators, A, B and C at factory I and factory II. The company has orders for atleast 6400 calculators of model A, 4000 calculators of model 8 and 4800 calculators of model C. At  factory I, 50 calculators of model A, 50 of model 8 and 30 of model C are made everyday, at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs ? 12000 and 1 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.

Answer

N/a

Explanation

Let the factory I operate for x days and the factory II operate for y days. At factory l, 50 calculators of model A and at factory II, 40 calculators of model A are made everyday. Also, company has ordered for atleast 6400 calculators of model A.
`50x+40 ge 6400 Rightarrow 5x +4y ge 640 ,.....(i)`
Also, at factory l, 50 calculators of model 8 and at factory II, 20 calculators of modal 8 are made everyday Since, the company has ordered atleast 4000 calculators of model B
`therefore 50x+20y ge 4000 Rightarrow 5x+2y ge 4000 ...(ii)`
Similarly for model C, 30x+40y ge 4800
`Rightarrow 3x+4y ge 480 ...(iii)`
Also, `x ge 0, y ge 0 ...(iv)["Since x and y are non negative"]`
If costs 12000 and 15000 each day to operate factories I and II respectively.
Corresponding LPP is
Minimise Z=12000x+15000y, "subject to" `5x+6y ge 640`
`5x+2y ge 480`
`3x+4y ge 480`
`x ge 0, y ge 0`
on solving 3x+4y=480 and 5x+4y=640, we get x=80, y=60
On solving 5x+4y=640, we get x =32, y=120
Thus from the graph it is clear that feasible region is unbounded and the coordinates of corner points A,B,C and D are (160,0),(80,60),(32,120) and (0,200) respectively


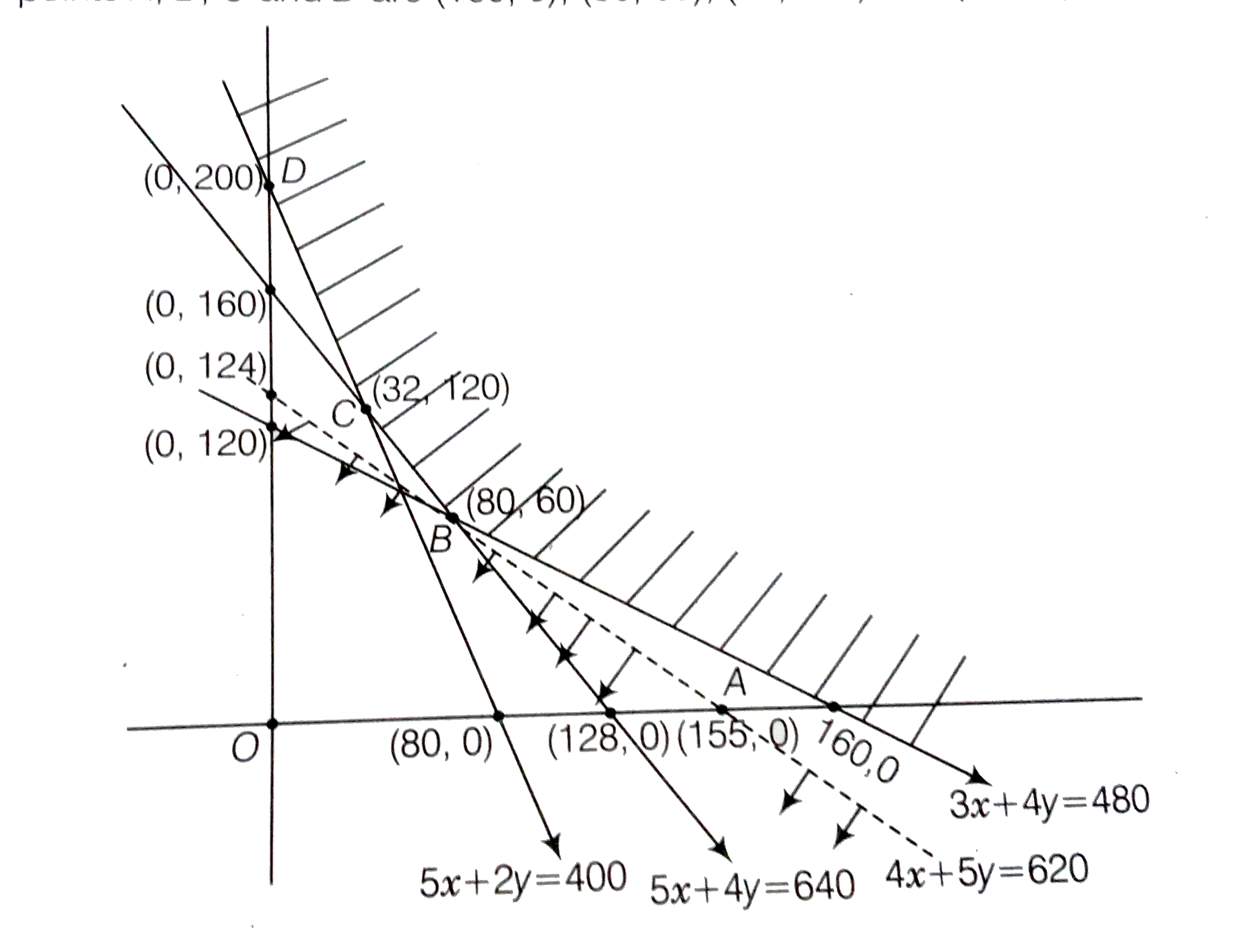
From the above table, it is clear that for given unbouded region the minimum valur of Z may or may not be 1860000.
Now for deciding this, we graph, the inequality
12000x+15000y lt 1860000
`4x+5y lt 620`
and check whether the resulting open half plane has points in common with feasible region or not. Thus, as shown in the figure it has no common points so, Z=12000x+15000y has minimum value 1860000. Som number of day factory I should be operated is 80 and number of days factory II should be operated is 60 for the minimum cost and satisfying the given constraints.