The feasible solution for a LPP is shown in following figure. Let Z=3x-4y be the objective function, Minimum of Z occurs at
(0,0)
(0,8)
(5,0)
(4,10)
The correct Answer is:B

Hence, the minimum of Z occurs at (0,8) and its minimum value is (-32)
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR PROGRAMMINGExercise:FILLERS
Explore 7 Videos
- LINEAR PROGRAMMINGBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR PROGRAMMINGExercise:TRUE/FALSE
Explore 2 Videos
- LINEAR PROGRAMMINGBook:NCERT EXEMPLAR ENGLISHChapter:LINEAR PROGRAMMINGExercise:TRUE/FALSE
Explore 2 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Fillers
Explore 18 Videos
- MATRICESBook:NCERT EXEMPLAR ENGLISHChapter:MATRICESExercise:Solved example
Explore 101 Videos
Similar Questions
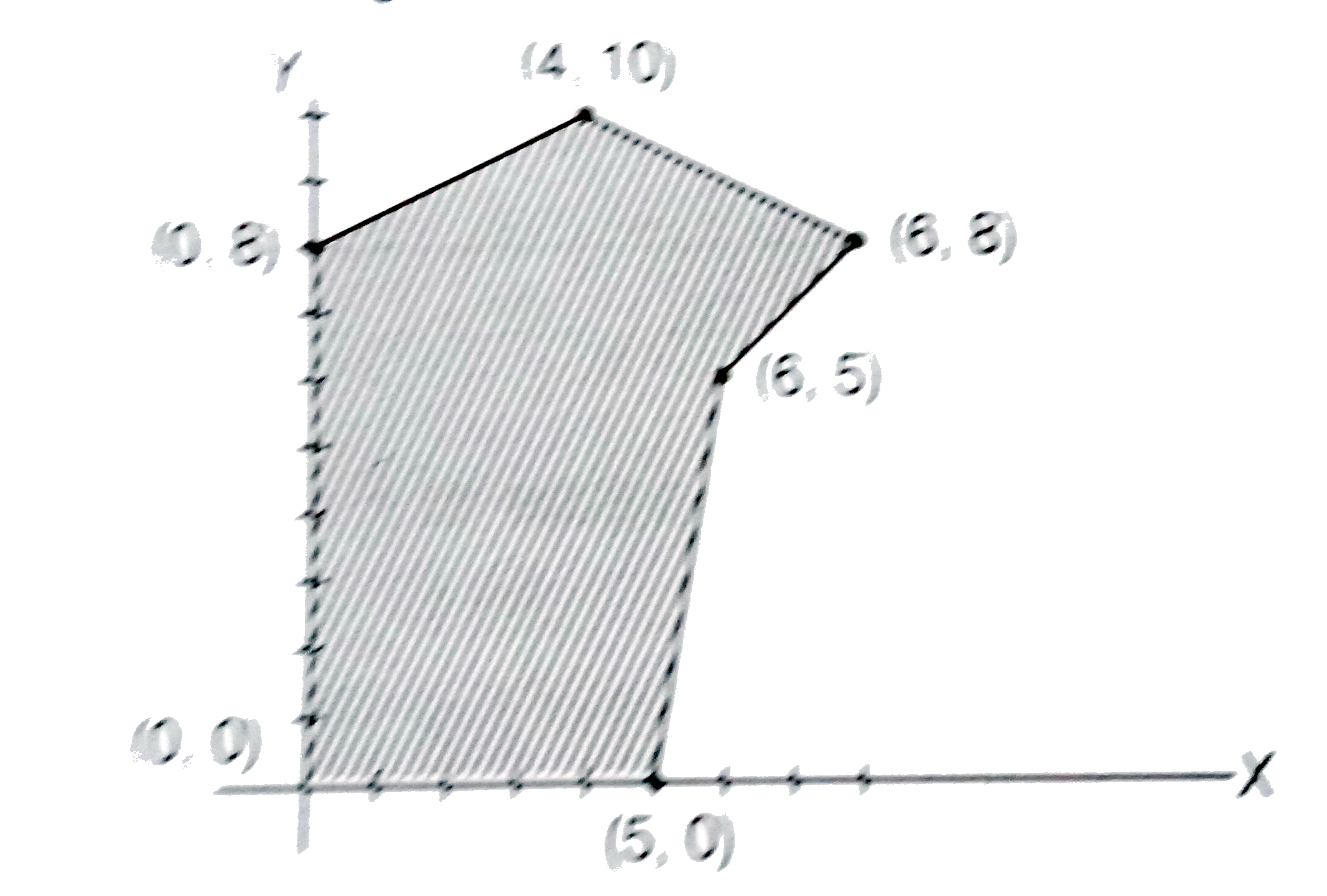
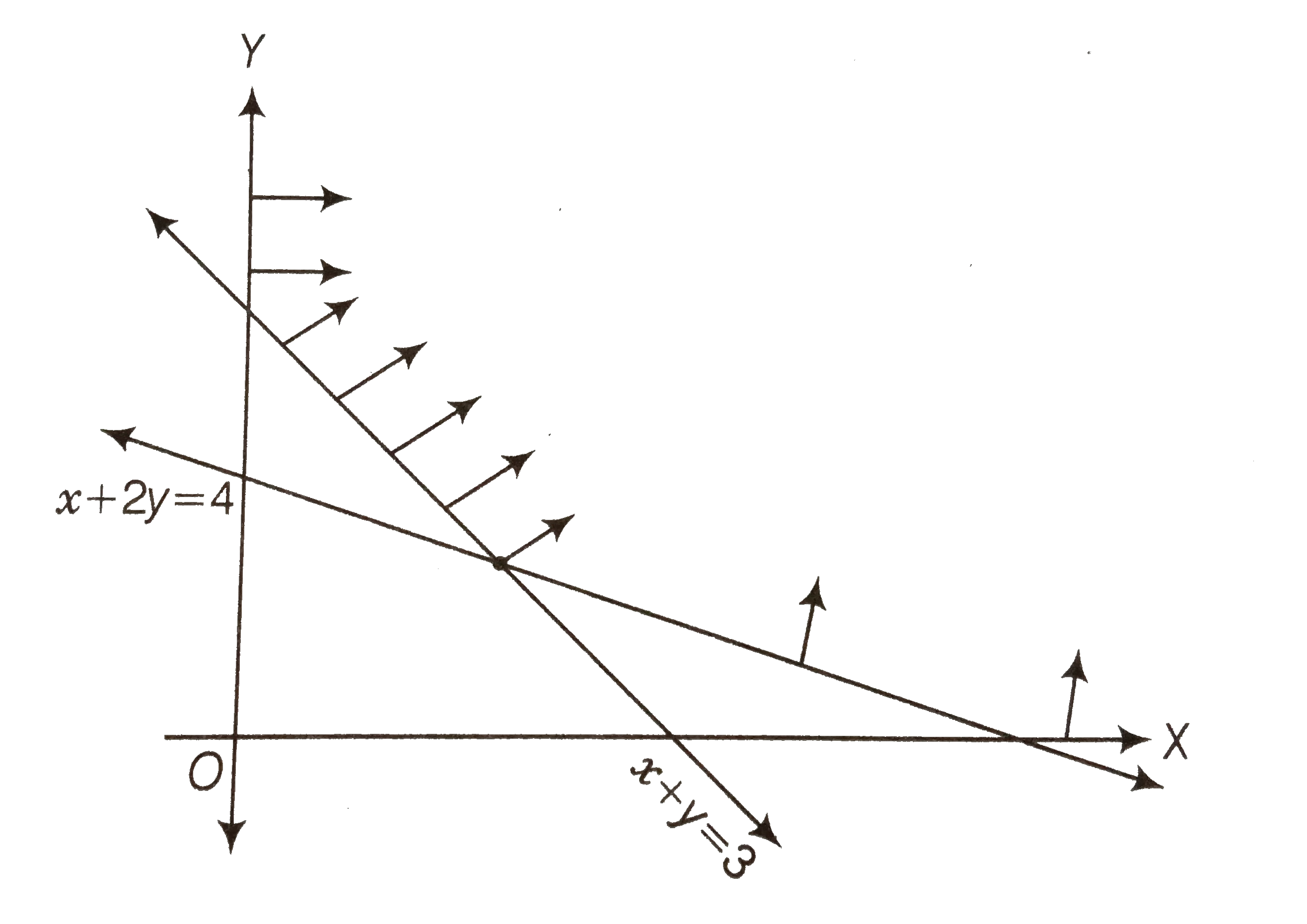
The feasible region for an LPP is shown in the following figure. Let F=3x−−4y be the objective function. Maximum value of F is
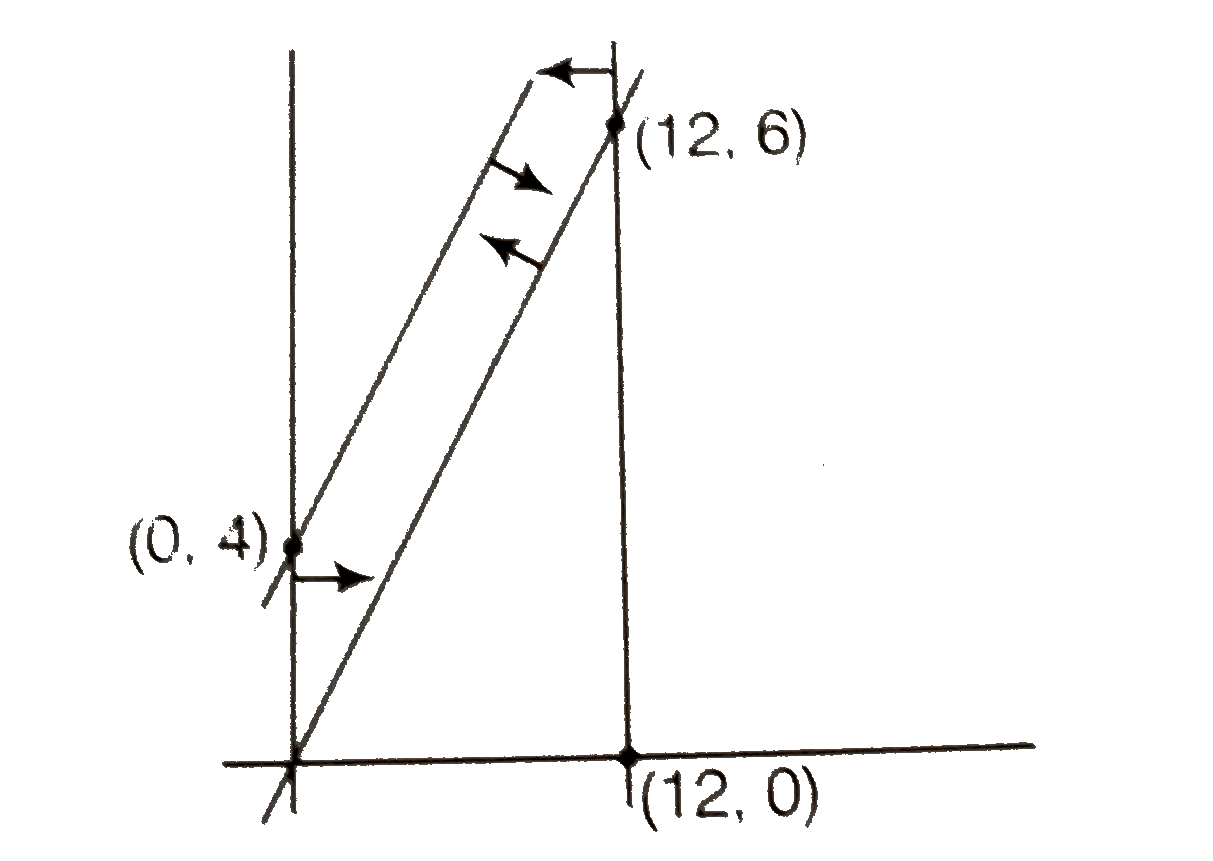
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.
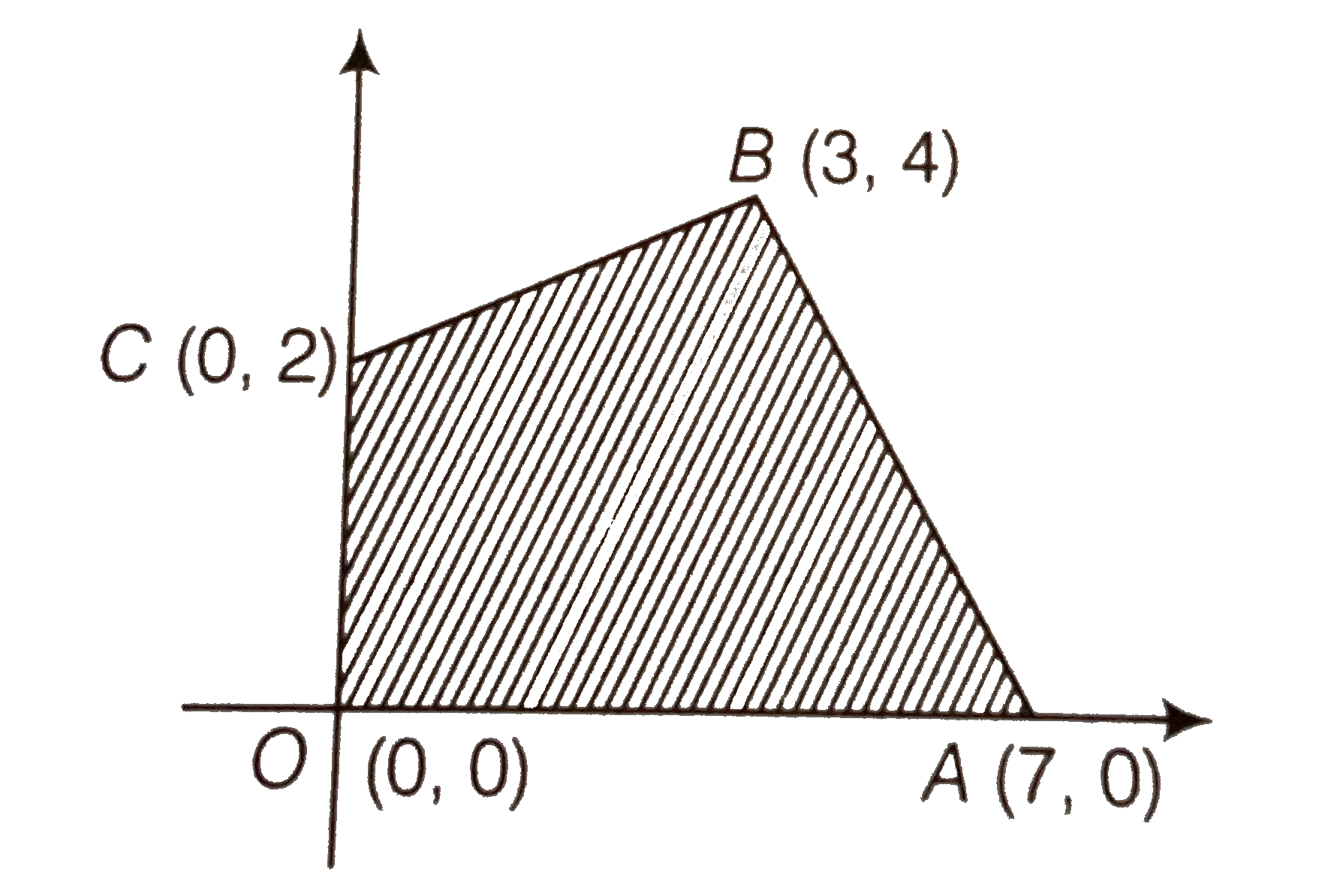
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
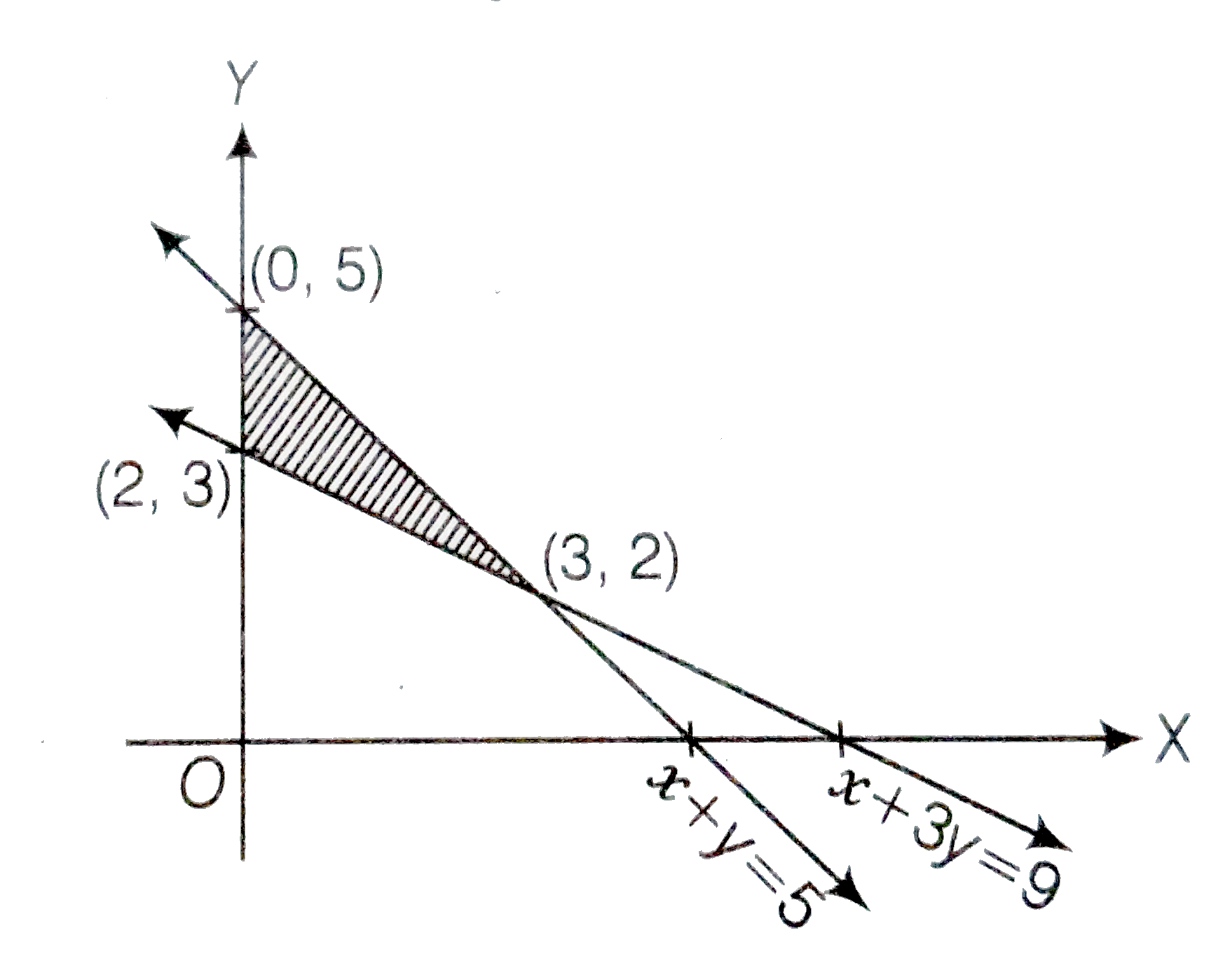
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists
View SolutionCorner points of the feasible region for an LPP are ( 0,2) (3,0) ,(6,0),(6,8) and (0,5) Let Z=4 x + 6y be the objective function. The minimum value of F occurs at?
View SolutionIf the feasibile region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionIn the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
View SolutionCorner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F-4x+6y be the objective function. Determine the minimum valur of F occurs at
View SolutionIn the given graph,the feasible region for a LPP is shaded. The objective function Z=2x−3y,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5)
View SolutionIn the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
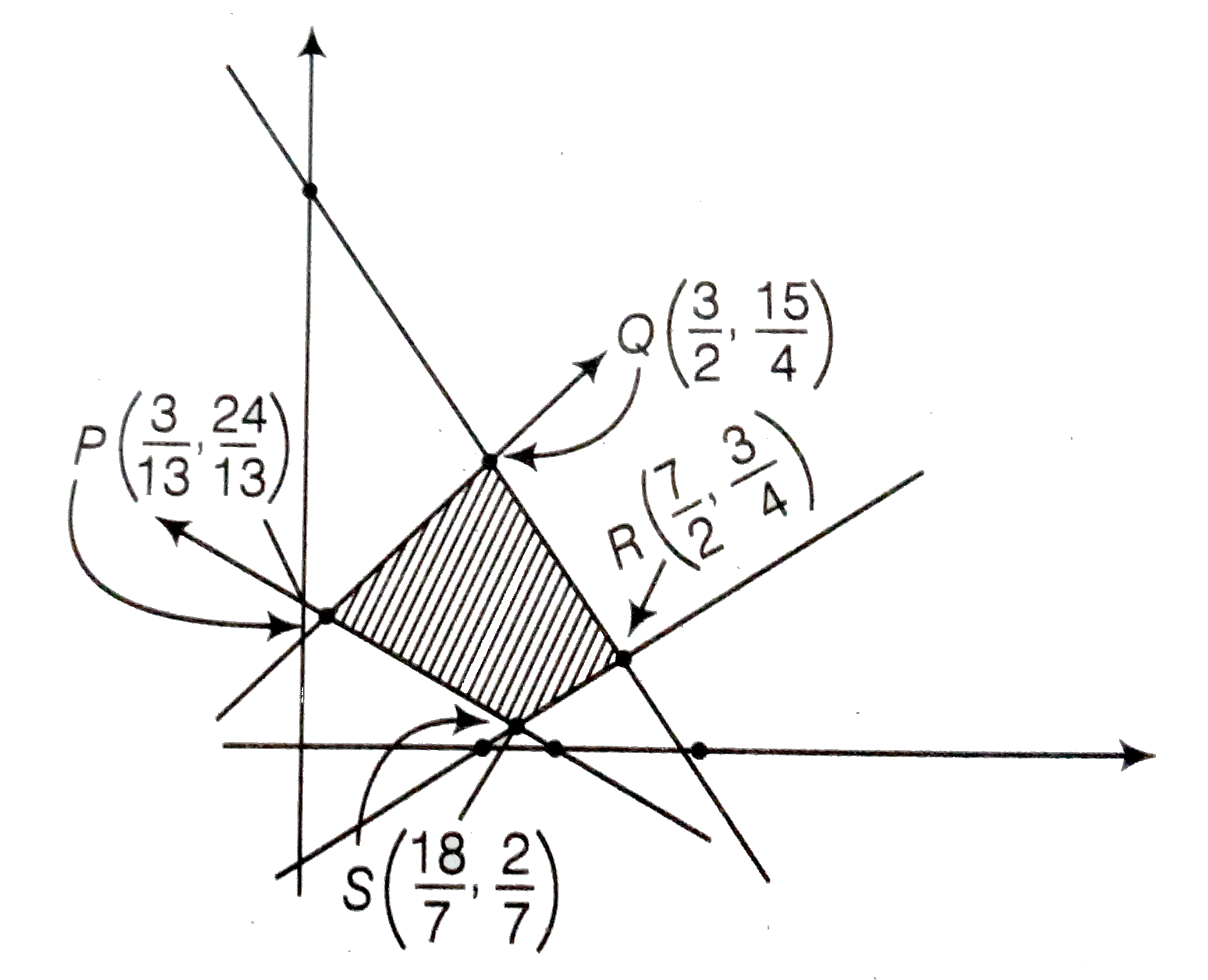
View Solution
